Mercury fills a glass tube Fig. so that the total column is 20 cm long. The tube is then rocked, so that the mercury begins to oscillate. Find the frequency and the period of the vibrations.

The correct Answer is:1.6Hz;0.63s.
AS may be seen from Fig the force which restores the body to its equilibrium positions is F=ρgΔV=2ρgSx. Since this force is proportional to the displacement, the natural frequency of the vibrations can be found from the formula ω0=√k/m. Here k=F/x=2ρgS,m=ρSl.
Hence ω0=√2g/l
Similar Questions
In given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View Solution
Knowledge Check
In a glass tube columns of water and mercury appear as shown.
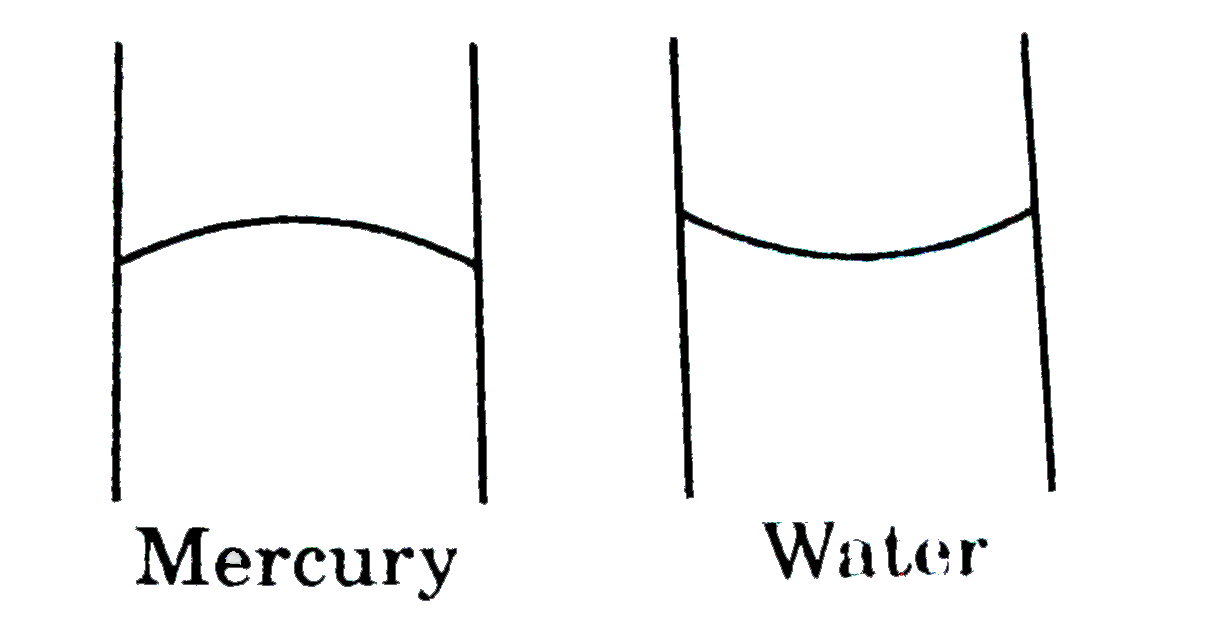
This is best attributed to the differences in their:AdensitiesBmolar massesCsurface tensionsDviscositiesWhat will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
A narrow uniform glass tube contains air enclosed by 15 cm long thread of mercury. When the tube is vertical with open end uppermost, the air column is 30 cm long. When the tube is inverted, the length of air column becomes 45 cm. Calculate the atmospheric pressure.
View Solutionthe height of mercury in a fauilty barometer is 75 cm and the tube above mercury is 10 cm long. The correct barometer reading is 76 cm. when the faulty barometer reads 74 cm, find the true barometer reading .
View SolutionAn open glass tube is immersed in mercury so that a length of 8cm of the tube projects above the mercury. The tube is then closed and raised through 44cm. What length of the tube will be occupied by the air after it has been raised? Given 1 atm =76cm of Hg.
View SolutionA glass tube with a sealed end is completely submerged in a vessel with mercury. The air column is 15 cm long. The what height (in cm) must the upper end be raised above the level of Hg so that the level of Hg inside the tube is at the level of Hg in the veseel ?
[Atmospheric pressure = 75 cm of Hg column]
View SolutionA glass tube sealed at one end and containing a quantity of air is immersed in mercury until the sealed end is 10 cm from the surface of mercury. At 0∘C the level of mercury in the tube is 5 cm above the level of mercury in the vessel. The length of the tube is 15 cm. To what temperature should the air in the tube be raised as to fill the tube completely? The atmospheric pressure is 75 cm of Hg. Neglect any change in the level of mercury in the vessel.
View SolutionA uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View Solution
