A mathematical pendulum 1 m long is deflected from the vertical by an angle of 40∘ and let go. Find the period of oscillations using numerical methods.
What will be the error, if in this case we use the formula for small oscillations?
The correct Answer is:2.08
The particle.s velocity at an arbitrary point on the circle is Fig
v−√2gh=√2gl(cosα−cosα0)=√2gl
where x=√cosα−cosα0. The body travels along the element of arc Δs=lΔα in time
Δl=Δsvnv=lΔαxav√2gl=Δαxn√2√lg
Put Δα=3∘=π/60 radian. Then
Δt=2π√1g.√2240xav
The period of oscillations is
T=4(Δt1+Δt2+......)=2π√lg√260(1x1av+1x2av+)

Since the formula T0=2π√l/g is used to compute the period of small oscillations, it follows that T=kT0, where
k=√260(1x1av+1x2av+.........)
is the correction factor. Let us compile a table from the computed data. We have
k=√2×44.2360=1.042
Hence, the period T=2πk√l/g=2.08 s, the value of T0 being T02π√l/g=2.00 s. In this case the relative error due to the use of the formula for small oscillations will be 4%.
Similar Questions
If the length and time period of an oscillating pendulum have errors of 1% and 2% respectively,what is the % error in the estimate of g?
View SolutionA hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum . How does it differ from the time period calculated using the formula for a simple pendulum?
View Solution
Knowledge Check
A simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m/s2 is (use g=10m/s2)
Aπ√5 sB√25πsCπ√2 sDπ√3 sA carriage is sliding down an inclined plane at an angle of 60° with a simple pendulum of length 1 m, its period of oscillation will be
A2sB1sC0.5sD0.45sThe length of a simple pendulum is about 100 cm known to an accuray of 1 mm. its period of oscillation oscillations using a clock of 0.1 resolution. What is the accuray in the determined value of g?
A0.2%B0.5%C0.1%D2%
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum . How does it differ fro the time period calculated using the formula for a simple pendulum?
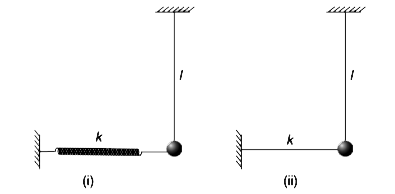
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
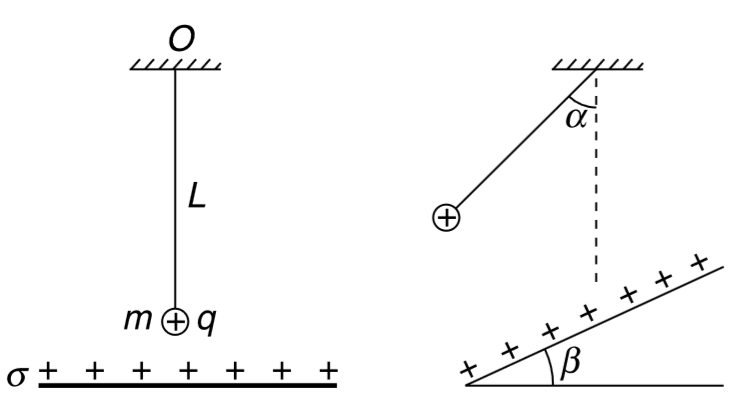
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View SolutionA horizontal platform with a small object placed on it executes a linear SHM in the vertical direction. The amplitude of oscillation is 40 cm. What should be the least period of these oscillation, so that the object is not detached from the platform ? [ Use g=10m/s2]
View Solution
