What is Plank length?
Step-by-Step Solution:
1. Definition of Planck Length:
The Planck length is defined as the smallest measurable length in the universe. It is a fundamental physical constant that represents a scale at which classical ideas about gravity and space-time cease to be valid.
2. Value of Planck Length:
The numerical value of the Planck length is approximately 1.616255×10−35 meters. This indicates that the Planck length is extremely small, far beyond the scale of everyday measurements.
3. Discovery:
The concept of Planck length was introduced by physicist Max Planck, who is also known for his work in quantum theory.
4. Formula for Planck Length:
The Planck length can be calculated using the formula:
lp=√h⋅Gc3
where:
- lp = Planck length
- h = Planck's constant (6.62607015×10−34Js)
- G = Universal gravitational constant (6.67430×10−11m3kg−1s−2)
- c = Speed of light in vacuum (3×108m/s)
5. Significance of Planck Length:
The Planck length is significant in the fields of quantum mechanics and general relativity. It is theorized that at scales smaller than the Planck length, the conventional laws of physics may not apply, and quantum gravitational effects become significant.
The Planck length is defined as the smallest measurable length in the universe. It is a fundamental physical constant that represents a scale at which classical ideas about gravity and space-time cease to be valid.
The numerical value of the Planck length is approximately 1.616255×10−35 meters. This indicates that the Planck length is extremely small, far beyond the scale of everyday measurements.
The concept of Planck length was introduced by physicist Max Planck, who is also known for his work in quantum theory.
The Planck length can be calculated using the formula:
lp=√h⋅Gc3
where:
- lp = Planck length
- h = Planck's constant (6.62607015×10−34Js)
- G = Universal gravitational constant (6.67430×10−11m3kg−1s−2)
- c = Speed of light in vacuum (3×108m/s)
The Planck length is significant in the fields of quantum mechanics and general relativity. It is theorized that at scales smaller than the Planck length, the conventional laws of physics may not apply, and quantum gravitational effects become significant.
Topper's Solved these Questions
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (VERY SHORT ANSWER TYPE)
11 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (LONG ANSWER QUESTIONS)
9 Videos
- THERMAL RADIATION BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
14 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
Two persons A and B are standing at the two opposite ends of a plank of length 4 m as shown in the figure. Plank is kept on a frictionless horizontal surface. Displacement of Plank, when A and B interchange their positions on the plank is (given mA=40 kg, mB=60 kg, mplank=20 kg)
_PHY_E05_138_Q01.png)
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View Solution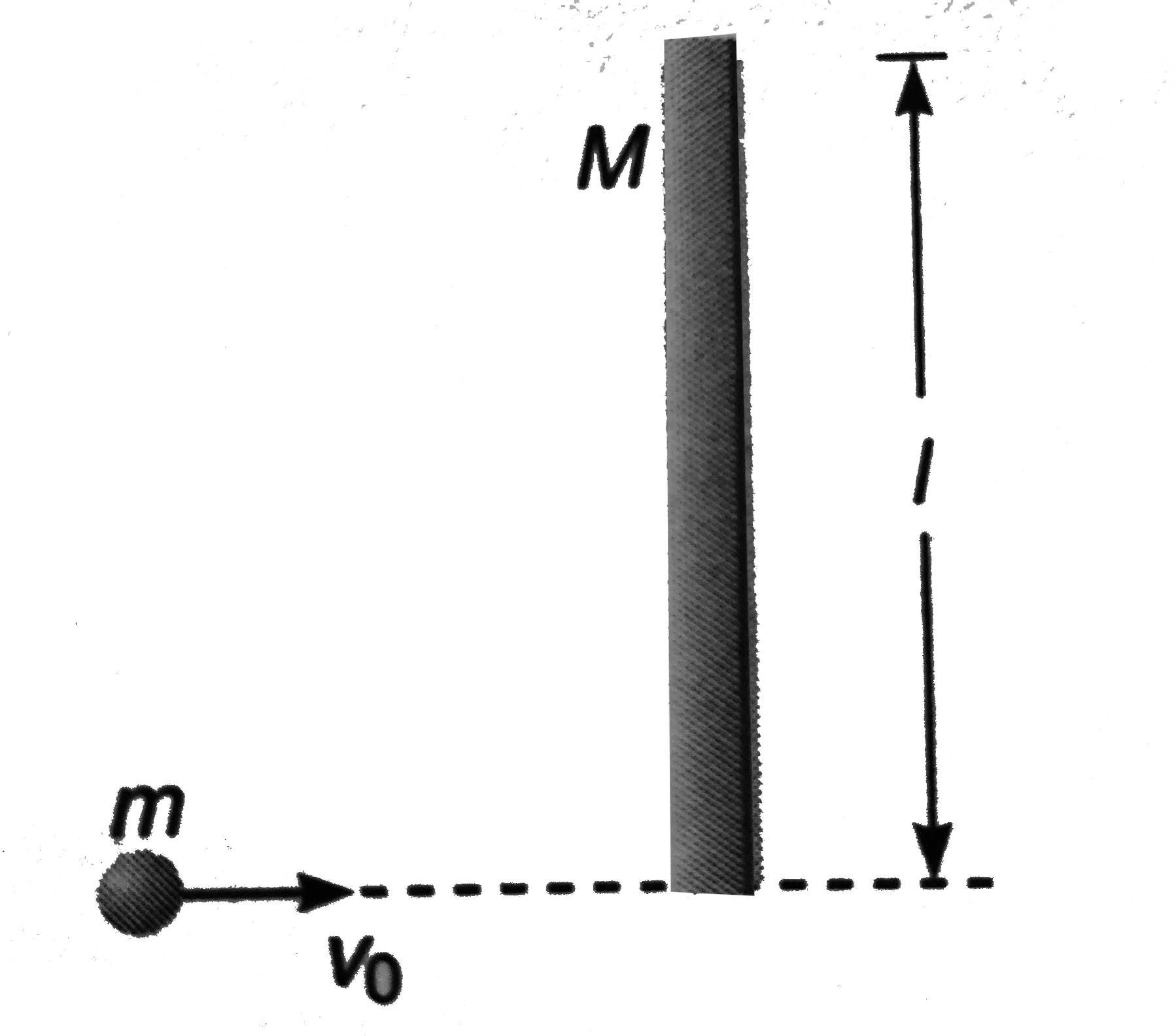
A boy mass m runs on ice with velocity v and steps on the end of a plank of length l and mass M which is perpendicular to his path.
(a). Describe quantitatively the motion of the system after the boy is on the plank. Neglect friction with the ice.
(b). One point on the plank is at rest immediately after the collision. Where is it?
View SolutionTwo men A and B are sitting at th eend of a plank of length L, if plank is rotating with angular velocity ω about an axis perpendicular to its length and passing through a point at a distance of L/3 from A. The angular velocity of B with respect to A is
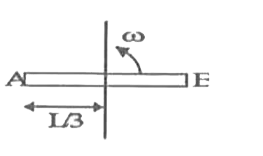
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA bullet loses 1/20 of its velocity in passing through a plank. What is the least number of plank required to stop the bullet .
View Solution
