The resistance R of a metallic conductor is equal to the ratio of potential difference V across the resistor to the current I through the conductor. Calculate R given tat V=(11.1±0.1) volt and I=(5.5±0.5)A
The correct Answer is:(2.02±0.2O)Ω
(ΔA/A)×100%=(Δl/l)×100%+(Δb/b)×100%.
2.2=(0.1/l)100+(0.1/7.9)100, solving l=10.6 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (VERY SHORT ANSWER TYPE)11videos
UNITS
- BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)14videos
THERMAL RADIATION
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
How are the potential difference (V), current (I) and resistance (R) related ?
View SolutionFor a metallic wire, the ratio Vi ( V= applied potential difference and i= current flowing ) is
View SolutionCalculate the potential difference required across a conductor of resistance 5 Ω to pass a current of 1.5 A through it.
View SolutionCalculate the potential difference across the ends of a wire of resistance 2Ω'whenacurrentof1.5 A passes through it.
View SolutionThe potential difference V across and the current I flowing through an instrument in an AC circuit are given by:
V=5cosωt volt
I=2sinωt Amp.View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
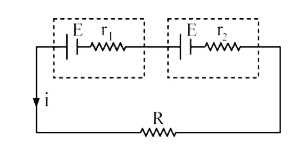
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionDraw a labelled circuit diagram to study the dependence of current (I) on the potential
difference (V) across a resistor.View SolutionA current of 0.2 A flows through a wire whose ends are at a potential difference of 15 V. Calculate :
the resistance of the wire,View SolutionFor a given metallic conductor , the variation of current through the conductor with potential difference applied across the conductor is shown in the given graph. If temperature of the conductor is increased , then slope tan theta
_PHY_E01_0010_Q01.png)
View Solution