A resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
To find the relation between the EMF of the cell (e), the potential difference across the resistor (V), the resistance of the resistor (R), and the internal resistance of the cell (r), we can follow these steps:
1. Understanding the Circuit:
- We have a cell with an EMF (e) and an internal resistance (r).
- A resistor (R) is connected to this cell.
- The potential difference across the resistor is denoted as (V).
2. Applying Ohm's Law:
- The current (I) flowing through the circuit can be expressed using Ohm's Law. The total EMF (e) is equal to the total voltage drop across the circuit.
- The total resistance in the circuit is the sum of the internal resistance (r) and the external resistance (R). Therefore, the total resistance is (R + r).
3. Calculating Current (I):
- According to Ohm's Law, the current can be calculated as:
I=eR+r
4. Finding the Potential Difference (V):
- The potential difference across the resistor (R) can be expressed as:
V=I⋅R
- Substituting the expression for current (I) from the previous step:
V=(eR+r)⋅R
5. Final Relation:
- Rearranging the equation gives us the final relation:
V=eRR+r
Conclusion:
The relation between the EMF (e), the potential difference across the resistor (V), the resistance of the resistor (R), and the internal resistance (r) is given by:
V=eRR+r
- We have a cell with an EMF (e) and an internal resistance (r).
- A resistor (R) is connected to this cell.
- The potential difference across the resistor is denoted as (V).
- The current (I) flowing through the circuit can be expressed using Ohm's Law. The total EMF (e) is equal to the total voltage drop across the circuit.
- The total resistance in the circuit is the sum of the internal resistance (r) and the external resistance (R). Therefore, the total resistance is (R + r).
- According to Ohm's Law, the current can be calculated as:
I=eR+r
- The potential difference across the resistor (R) can be expressed as:
V=I⋅R
- Substituting the expression for current (I) from the previous step:
V=(eR+r)⋅R
- Rearranging the equation gives us the final relation:
V=eRR+r
The relation between the EMF (e), the potential difference across the resistor (V), the resistance of the resistor (R), and the internal resistance (r) is given by:
V=eRR+r
Similar Questions
A capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View SolutionA cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png) View Solution
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionA resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell is V. Write the expression for r in terms of ε, V and R.
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionThe figure shows a network in which the cell is deal and it has an emf E. The potential difference across the resistance 2R is
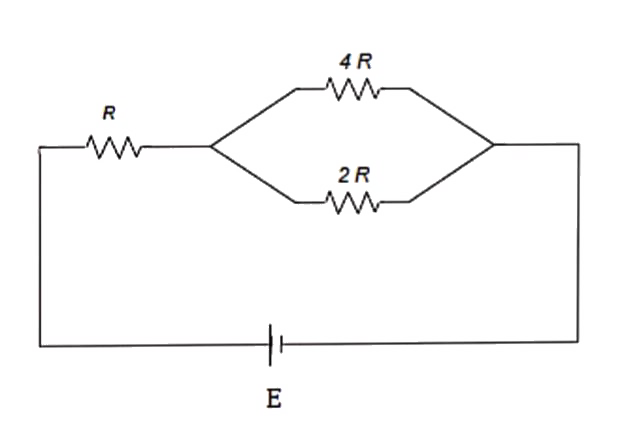 View Solution
View Solution(a) A voltmeter with resistance Rv is connected across the terminals of a battery of emf E and internal resistance r. Find the potential difference measured by the voltmeter.
(b) IfE=7.50V and r=0.45Ω, find the minimum value of the voltmeter resistance Rv so that the voltmeter reading is within 1.0% of the emf of the battery. (c) Explain why your answer in part (b) represents a minimum value.View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
 View Solution
View SolutionA resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
View Solution

