The resultant of two vectors →Aand→B is perpendicular to →A and equal to half of the magnitude of →B. Find the angle between VecAandVecB?
Since →R is perpendicular to →A. Figure shows the three vectors →A,→Band→R.
angle between →Aand→B is p-q
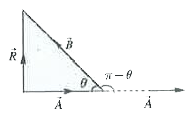
sinq=RB=B2B=12
⇒q=30∘⇒ angle between A and B is 150∘.
Similar Questions
The resultant of two vectors →A and →B is perpendicular to →A and equal to half of the magnitud of →B. Find angle between →B and →B?
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View Solution
Knowledge Check
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-
A120∘B150∘C135∘DNone of theseThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .A120B90C60D150
.A120B90C60D150The resultant of →A and →B is perpendicular to →A. What is the angle between →A and →B ?
Acos−1(AB)Bcos−1(−AB)Csin−1(AB)Dsin−1(−AB)
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .
.
View SolutionThe resultant of →A and →B is perpendicular to →A. What is the angle between →A and →B ?
View SolutionThe resultant of →A and →B is perpendicular to →A. What is the angle between →A and →B ?
View SolutionTwo vectors →Aand→B have equal magnitudes.If magnitude of (→A+→B) is equal to n times of the magnitude of (→A−→B) then the angle between →Aand→B is :-
View SolutionTwo vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-
View Solution
