Two pesons P and Q crosses the river starting from point A on side to excatly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The persons Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
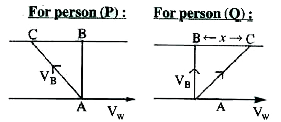
tp=d√V2B−V2W=d√52−32=d4
tq=dVB=d5,tP=tQ+Δt
d4=d5+xVman, Butx=VWdVB
(d)/(4)=(d)/(5)+(V_(W)d)/(V_(B)V_(man))," "(canceld)/(4)=(canceld)/(5)+(3canceld)/((5)V_(man))
14−15=35Vman, 120=35Vman
Vman=(3)(20)5=12kmph
Similar Questions
Two persons P and Q crosses the river starting from point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5 kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
View SolutionTwo persons P and Q crosses the river starting the point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B.Velocity of river is 3kmph and speed of each person is 5kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is .
View Solution
Knowledge Check
A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
A9.4B2C84.6D28.2A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
AThe direction of boat's velocity is 30∘ west of north.BThe direction of boat's velocity is north - west.CResultant velocity is 5ms−1.DResultant velocity of boat is 5√2ms−1.
(A): A man is on the northern bank of a river. To cross the river in a shortest time he should swim due south.
(R) : Man should move opposite to the river flow to cross in shortest time.
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA man can swim in still water at a speed of 6 kmph and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of 3 kmph, and the width of the river is 2 km, the time taken to cross the river is (in hours)
View SolutionA man crosses a river in a boat. If he cross the river in minimum time he takes 10min with a drift 120m. If he crosses the river taking shortest path, he takes 12.5min, find
(a) width of the river
(b) velocity of the boat with respect to water
(c) speed of the current
View Solution
