A stone is thrown horizontally from a height with a velocity $v_{9} x) = 15 m / s$ . Determine the normal and tangetial acceleartion of the stone in 1 second after begins to move.

Text Solution

Verified by Experts

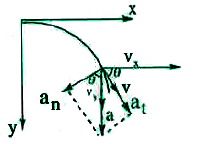
The horizontal component of acceleration is zero. The net acceleration of the stone is directed vertically downward and is equal to the acceleration due to gravity g. Thus $a = g = \sqrt{a_{1}^{2} + a_{n}^{2}}$
from figure we can see that
$cos θ = \frac{V_{x}}{V} = \frac{a_{c}}{a} = \frac{a_{g}}{g}$ and $sin θ = \frac{V_{y}}{v} = \frac{a_{t}}{a} = \frac{a_{t}}{g}$
Hence $a_{t} = \frac{g (V_{y})}{V} = \frac{g^{2} t}{\sqrt{v_{x}^{2} + g^{2} t^{2}}}$ and $a_{c} = g \frac{v_{x}}{v} = \frac{g v_{x}}{\sqrt{v_{x}^{2} + g^{2} t^{2}}}$
on substituting numerical values,
$v_{x} = 15 m / s, g = 9.8 m / s^{2}$ ,
we get $a_{t} = 5.4 m / s^{2} and a_{n} = 8.2 m / s^{2}$

Updated on:21/07/2023

A stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A $2.2 m s^{- 1}$
B $3.3 m s^{- 1}$
C $4.4 m s^{- 1}$
D $1.1 m s^{- 1}$
A stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A $2.2 m s^{- 1}$
B $3.3 m s^{- 1}$
C $4.4 m s^{- 1}$
D $1.1 m s^{- 1}$
Two stones are thrown vertically upwards with the same velocity of $49 m / s$ . If they are thrown one after the other with a time lapse of 3 second, height at which they collide is
A58.8 m
B111.5 m
C117.6 m
D122.5 m