The x-component of the resultant of several vectors
(a) is equal to the sum of the x-components of the vecotrs
(b) may be smaller than the sum of the magnitudes of the vectors
( c) may be greater than the sum of the magnitudes of the vectors
(d) may be equal to the sum of the magnitudes of the vectors
only a
a, b & d
a, b, & c
b & d
The correct Answer is:B
Similar Questions
The sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
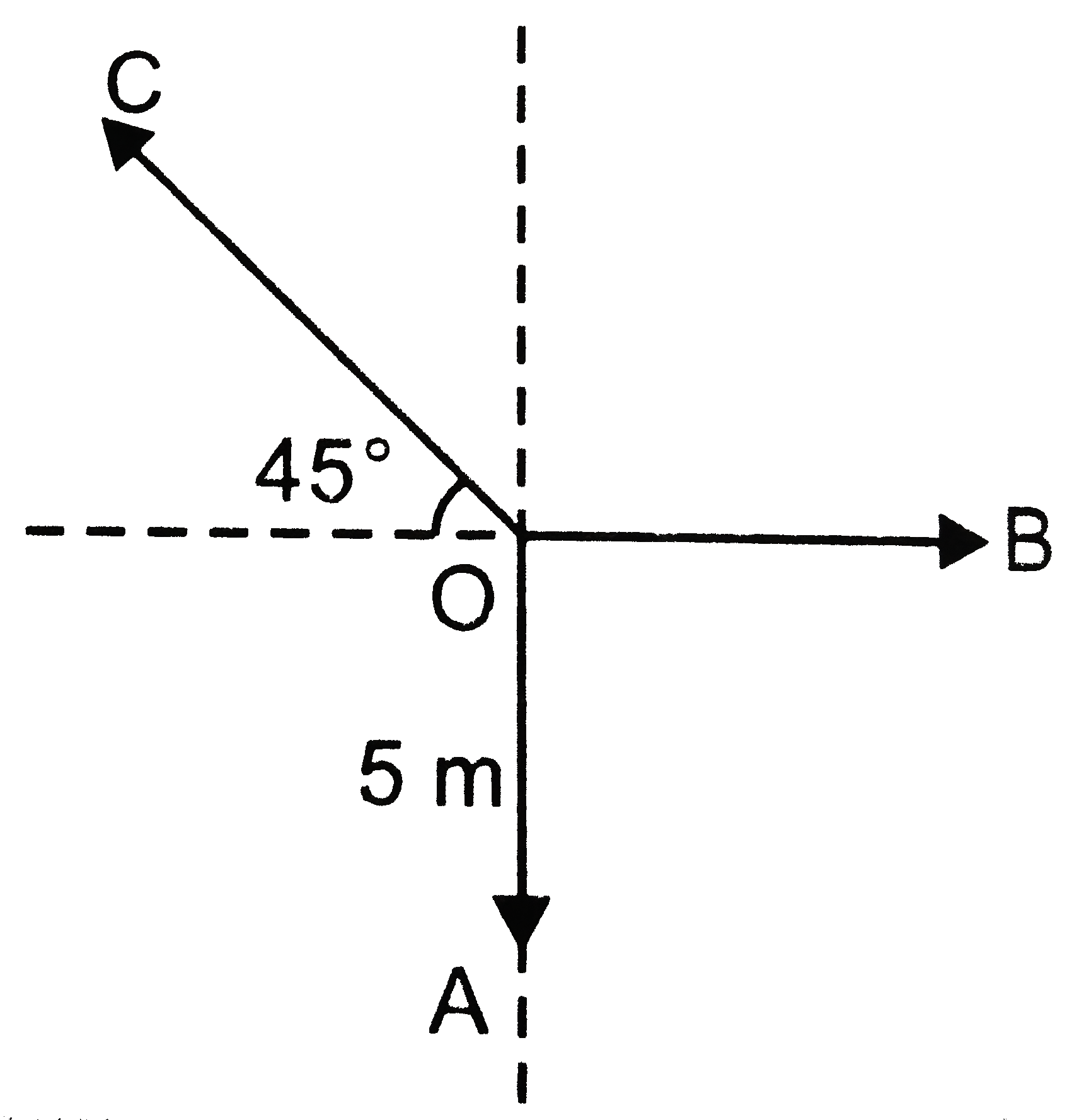 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View Solution
Knowledge Check
The x- component of the resultant of several vectors
(i) is equal to the sum of the x-components of the vectors
(ii) may be smaller than the sum of the magnitudes of the vectors
(iii) may be greater than the sum of the magnitudes of the vectors
(iv) may be equal to the sum of the magnitudes of the vectorsA(i),(ii)B(i),(ii),(iv)C(ii),(iii),(iv)Dall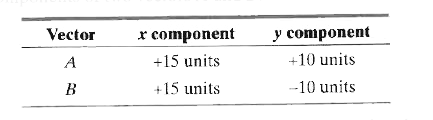
Determine the magnitude of the vector sum, A+B.A5 unitsB15 unitsC20 unitsD30 unitsThe sum of the magnitudes of two vectors P and Q is 18 and the magnitude of their resultant is 12. If the resultant is perpendicular to one of the vectors, then the magnitudes of the two vectors are
A5,13B8,10C7,11D12,6
If the sum of two unit vectors is a unit vector,then find the magnitude of their differences.
View SolutionCan any of the components of a given vector have greater magnitude than that of the vector itself ?
View SolutionThe magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
View SolutionThe magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
View SolutionIf the sum of two unit vectors is a unit vector, then the magnitude of their difference is :
View Solution
