The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
3
4
5
8
The correct Answer is:B
To find the magnitude of the y-component of vector →A, we can use the relationship between the components of the vector and its magnitude. Here are the steps to solve the problem:
1. Identify the components and magnitude:
- The x-component of vector →A is given as Ax=3.
- The magnitude of vector →A is given as |→A|=5.
- We need to find the y-component Ay.
2. Use the formula for the magnitude of a vector:
The magnitude of a vector in two dimensions can be expressed as:
|→A|=√A2x+A2y
3. Substitute the known values into the formula:
Plugging in the values we have:
5=√32+A2y
4. Square both sides to eliminate the square root:
52=32+A2y
This simplifies to:
25=9+A2y
5. Rearrange the equation to solve for A2y:
A2y=25−9
A2y=16
6. Take the square root to find Ay:
Ay=√16=4
7. Conclusion:
The magnitude of the y-component of vector →A is Ay=4.
Final Answer:
The magnitude of the y-component of vector →A is 4.
---
- The x-component of vector →A is given as Ax=3.
- The magnitude of vector →A is given as |→A|=5.
- We need to find the y-component Ay.
The magnitude of a vector in two dimensions can be expressed as:
|→A|=√A2x+A2y
Plugging in the values we have:
5=√32+A2y
52=32+A2y
This simplifies to:
25=9+A2y
A2y=25−9
A2y=16
Ay=√16=4
The magnitude of the y-component of vector →A is Ay=4.
The magnitude of the y-component of vector →A is 4.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS6videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS9videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
Similar Questions
The sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
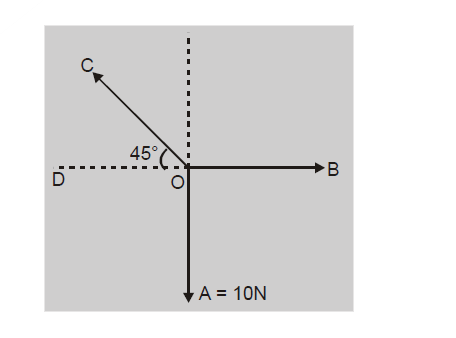
(ii) What is the magnitude of vector −−→OC ?View Solution→A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 →A ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
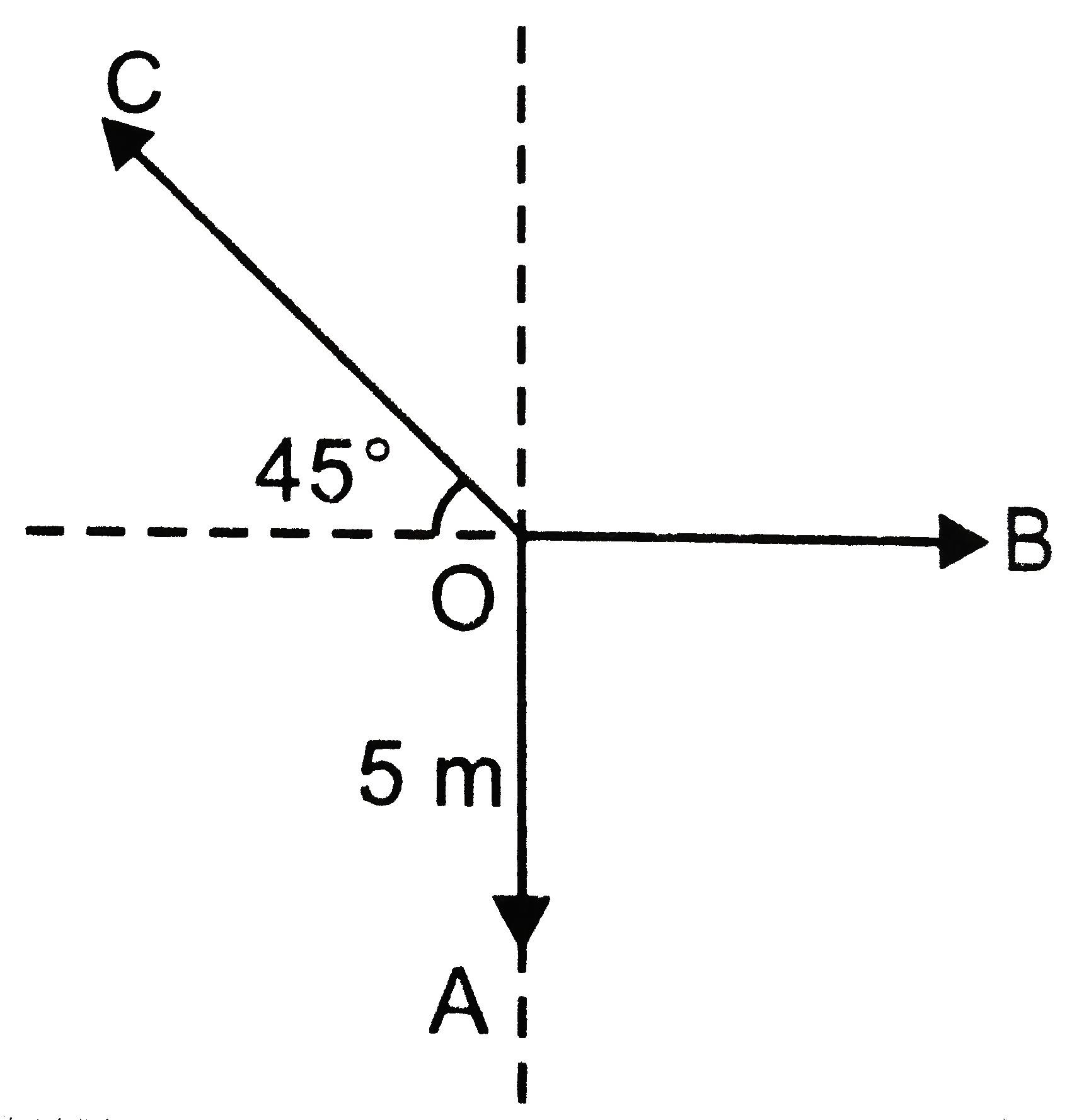 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?View SolutionThe x− component of a certain vector in x−y plane is 2 units and y− component is +2√3 units. What is the magnitude of the vector.
View SolutionThe magnitude of x and y components of →A are 7 and 6 respectively . Also , the magnitudes of x and y components of →A+→B are 11 and 9 respectively . Calculate the magnitude of vector →B
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 View Solution
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
 View Solution
View SolutionX- component of →a is twice of its Y- component. If the magnitude of the vector is 5√2 and it makes an angle of 135∘ with z-axis then the components of vector is:
View SolutionTwo vectors →A and →B have equal magnitudes . If magnitude of →A+→B is equal to n× the magnitude of →A−→B , then the angle between →A and →B is
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View Solution

