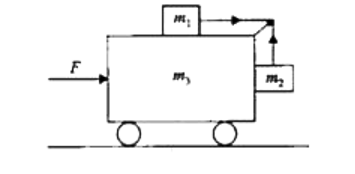
In m1=1kg, m2=2kg and m3=10kg. Find the horizontal force F that must be continuously applied on the system to m3 so that m1 and m2 do not move relative to m3. (Assume that the whole system is friction less).
The correct Answer is:254.8N
a=F/m1+m2+m1, Also T=m1a=m2g, a=(m2/m1)g, F=(m1+m2+m3)(m2/m1)g, F=(1+2+10)(2/1)×9.8=254.8N
Topper's Solved these Questions
Similar Questions
Knowledge Check
All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–
 A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2
A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2If m1=10kg,m2=4kg,m3=2kg, the acceleration of system is
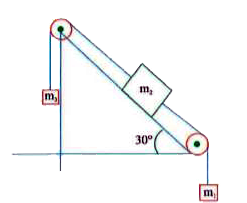 A5g/2B5g/3C5g/8D5g/14
A5g/2B5g/3C5g/8D5g/14If m1=10kg,m2=4kg,m3=2kg, the acceleration of system is
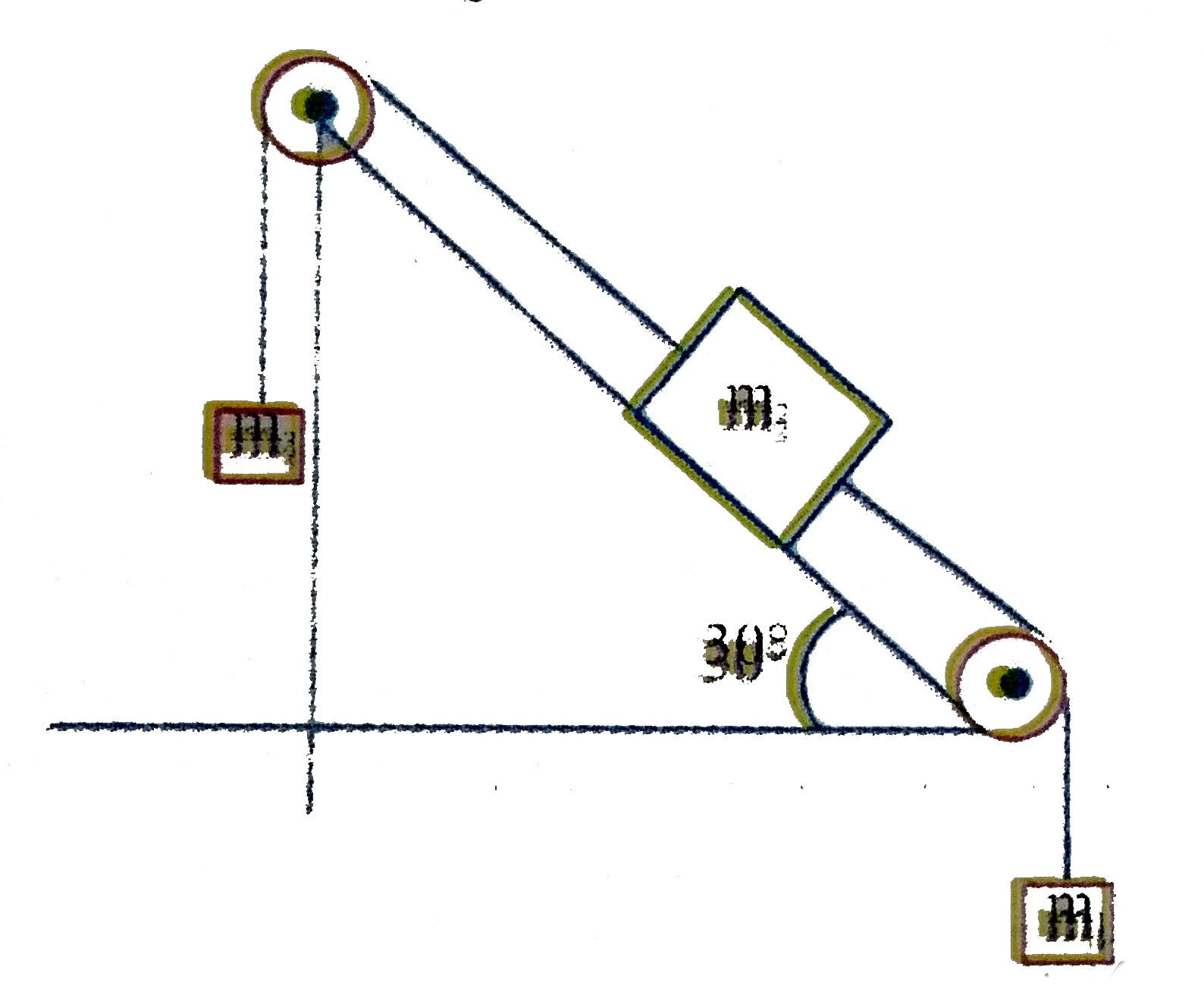 .A5g/2B5g/3C5g/8D5g/14
.A5g/2B5g/3C5g/8D5g/14
The tension in the string connected between blocks is

View SolutionLet m1=1kg, m2=2kg and m3=3kg in figure (5-E12).Find the accelerations of m1,m2 and m3 .The string from the upper pulley to m1 is 20cm when the system is released from rest.How long will it take before m1strikes the pulley?
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View SolutionThree block of masses m1=10kg,m2=20kg and m3=30kg are on a smooth horizontal table ,connected to each other by light horizontal string. A horizontal placed force F=60N is applied to m3, towards right find
(a) tensionT1 and T2 and
(b) tensionT2 if all of a sudden the string between m1 and m2 snaps.

View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View Solution