A vessel of length l, breadth b and height h is filled completely with a liquid of density d (see figure) Calculate the thrust on each surface of the cube.
To calculate the thrust on each surface of a cuboidal vessel filled with a liquid of density d, we will analyze the forces acting on each surface due to the pressure exerted by the liquid.
1. Understand the Dimensions and Density:
- The vessel is a cuboid with dimensions:
- Length = l
- Breadth = b
- Height = h
- The liquid has a density d.
2. Identify the Surfaces:
- The cuboid has six surfaces:
- Top surface
- Bottom surface
- Two side walls (length l and height h)
- Two front and back walls (breadth b and height h)
3. Calculate Pressure at Different Heights:
- The pressure exerted by the liquid at a depth h is given by:
P=d⋅g⋅h
- Where g is the acceleration due to gravity.
4. Calculate Thrust on the Bottom Surface:
- The thrust (force) on the bottom surface is calculated using the pressure at the bottom:
Thrustbottom=P⋅A=(d⋅g⋅h)⋅(l⋅b)
- Thus, the thrust on the bottom surface is:
Thrustbottom=d⋅g⋅h⋅l⋅b
5. Calculate Thrust on the Top Surface:
- The pressure at the top surface (at height 0) is:
P=0
- Therefore, the thrust on the top surface is:
Thrusttop=0
6. Calculate Thrust on the Side Walls:
- For the side walls, the pressure varies linearly from 0 at the top to d⋅g⋅h at the bottom.
- The average pressure on the side walls is:
Pavg=0+(d⋅g⋅h)2=d⋅g⋅h2
- The thrust on one side wall (length l and height h):
Thrustside=Pavg⋅A=(d⋅g⋅h2)⋅(h⋅b)
- Thus, the thrust on each side wall is:
Thrustside=d⋅g⋅h2⋅(h⋅b)
7. Calculate Thrust on the Front and Back Walls:
- Similarly, for the front and back walls (breadth b and height h):
Thrustfront/back=d⋅g⋅h2⋅(h⋅l)
Summary of Thrust on Each Surface:
- Bottom surface:
Thrustbottom=d⋅g⋅h⋅l⋅b
- Top surface:
Thrusttop=0
- Side walls (each):
Thrustside=d⋅g⋅h2⋅(h⋅b)
- Front and back walls (each):
Thrustfront/back=d⋅g⋅h2⋅(h⋅l)
- The vessel is a cuboid with dimensions:
- Length = l
- Breadth = b
- Height = h
- The liquid has a density d.
- The cuboid has six surfaces:
- Top surface
- Bottom surface
- Two side walls (length l and height h)
- Two front and back walls (breadth b and height h)
- The pressure exerted by the liquid at a depth h is given by:
P=d⋅g⋅h
- Where g is the acceleration due to gravity.
- The thrust (force) on the bottom surface is calculated using the pressure at the bottom:
Thrustbottom=P⋅A=(d⋅g⋅h)⋅(l⋅b)
- Thus, the thrust on the bottom surface is:
Thrustbottom=d⋅g⋅h⋅l⋅b
- The pressure at the top surface (at height 0) is:
P=0
- Therefore, the thrust on the top surface is:
Thrusttop=0
- For the side walls, the pressure varies linearly from 0 at the top to d⋅g⋅h at the bottom.
- The average pressure on the side walls is:
Pavg=0+(d⋅g⋅h)2=d⋅g⋅h2
- The thrust on one side wall (length l and height h):
Thrustside=Pavg⋅A=(d⋅g⋅h2)⋅(h⋅b)
- Thus, the thrust on each side wall is:
Thrustside=d⋅g⋅h2⋅(h⋅b)
- Similarly, for the front and back walls (breadth b and height h):
Thrustfront/back=d⋅g⋅h2⋅(h⋅l)
- Bottom surface:
Thrustbottom=d⋅g⋅h⋅l⋅b
- Top surface:
Thrusttop=0
- Side walls (each):
Thrustside=d⋅g⋅h2⋅(h⋅b)
- Front and back walls (each):
Thrustfront/back=d⋅g⋅h2⋅(h⋅l)
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS16videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - LONG ANSWER QUESTIONS5videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)21videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
Similar Questions
A hollow cylinder of radius R and length R is cut into four equal parts from its axis. Each one is called quarter cylinder. If the quarter cylinder is just completely immersed in a liquid of density ρ, find the horizontal thrust acting on the curved surface of the cylinder.
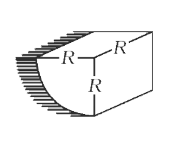 View Solution
View SolutionA vessel of base area 100 cm x 60 cm and height 200 cm is completely filled with a liquid of density 1.1×103kgm−3 Ignoring the atmosphere pressure find the thrust at the bottom of the vessel
View SolutionA vessel of base area 100cm×60cm and height 200cm is completely filled with a liquid of density 1.1×103kgm−3.
(a) Ignoring the atmospheric pressure, find :
(i) the thrust at the bottom of the vessel,
(ii) the pressure at the bottom of the vessel,
(iii) The pressure at a depth of 5 cm from the free surface,
(iv) the net force experienced by a metal foil of area 10cm2 placed at a depth of 5 cm from the free surface,
(b) The thrust at the bottom of the vessel if the atmospheric pressure equal to 1×105Nm−2 is taken into account.
Take g=9.8ms−2 .View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
View SolutionA wooden cube of length l and density a floats in a liquid of density p(>a). If the liquid moves with an acceleration in steady state, find the a. net hydrostatic force acting on the cube b. angle of inclination of the cub with horizontal.
 View Solution
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increasedView SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.
 View Solution
View SolutionA solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
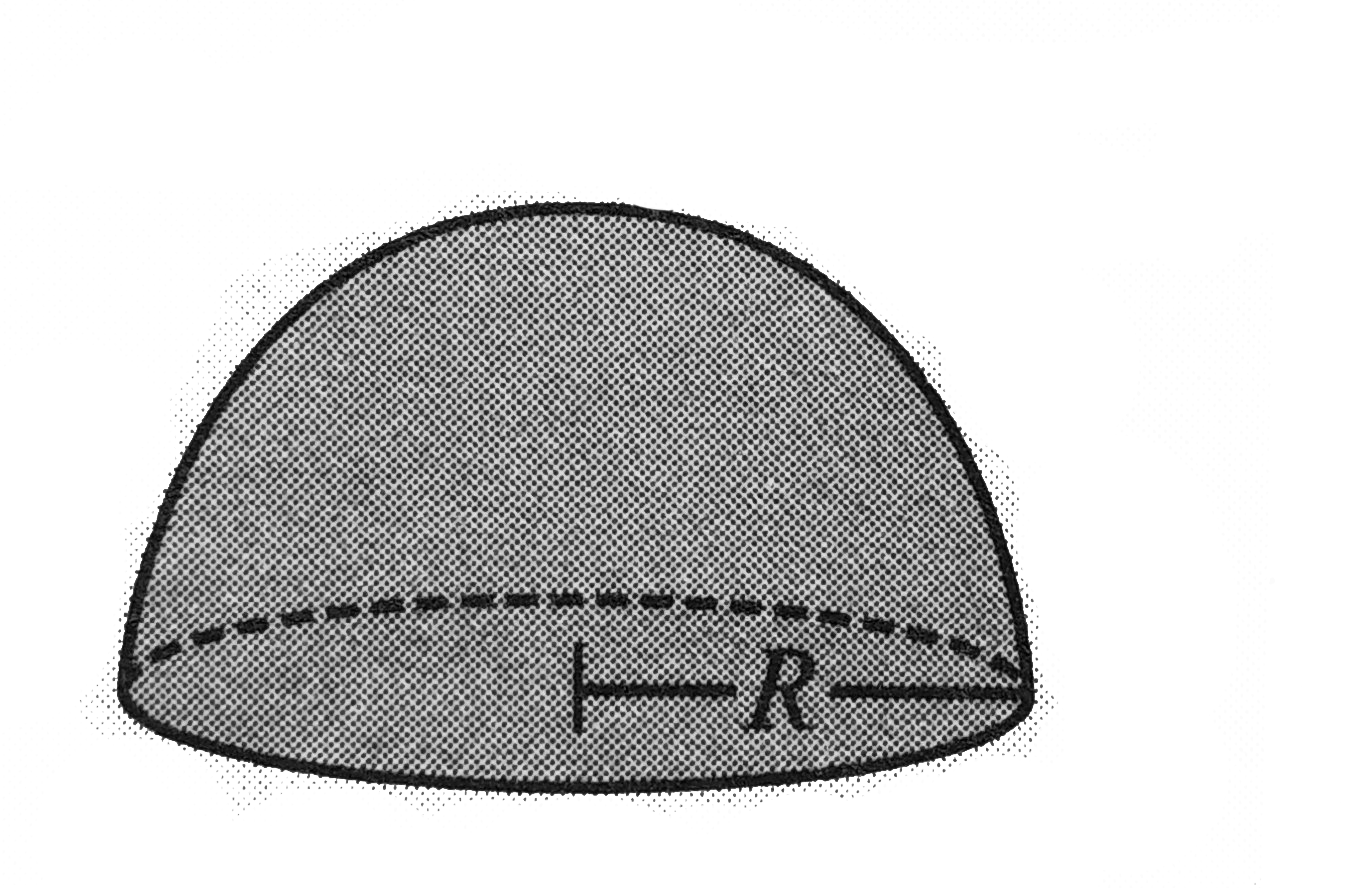 View Solution
View SolutionA person just observes the point A on the circumference at the bottom of an empty cylindricla vessel of diameter 10 cm . When the vessel is completely filled with a liquid (μ=√2), he can just see the centre B of the bottom. Then the height of the vessel is
 View Solution
View Solution

