A cube of side 4 cm is just completely immersed in a liquid A. When it is put in a liquid B, it floats with 2 cm outside the liquid. Calculate the ratio of densities of the two liquids.
The correct Answer is:1:2
To solve the problem, we need to analyze the situation in two different liquids: Liquid A and Liquid B. Let's break it down step by step.
Step 1: Understand the situation in Liquid A
When the cube is completely immersed in Liquid A, the buoyant force acting on it is equal to its weight.
- Weight of the cube (W): The weight of the cube can be expressed as:
W=Density of the cube×Volume of the cube×g
Since the cube is made of a uniform material, we can denote its density as ρc and its volume V as:
V=side3=4cm×4cm×4cm=64cm3
Thus, the weight of the cube is:
W=ρc×64cm3×g
- Buoyant force in Liquid A (F_bA): The buoyant force is equal to the weight of the liquid displaced, which is:
FbA=ρA×V×g=ρA×64cm3×g
Setting the weight equal to the buoyant force gives us:
ρc×64g=ρA×64g
From this, we can simplify to:
ρc=ρA
Step 2: Understand the situation in Liquid B
When the cube is placed in Liquid B, it floats with 2 cm of its height above the liquid. This means that 2 cm of the cube is above the surface, and the remaining part is submerged.
- Volume submerged in Liquid B (V'): The height submerged is:
Height submerged=Total height−Height above liquid=4cm−2cm=2cm
The volume submerged is:
V′=side2×height submerged=4cm×4cm×2cm=32cm3
- Buoyant force in Liquid B (F_bB): The buoyant force is now:
FbB=ρB×V′×g=ρB×32cm3×g
Setting the weight equal to the buoyant force gives us:
ρc×64g=ρB×32g
From this, we can simplify to:
ρc×64=ρB×32
Step 3: Relate the densities of the two liquids
Now we can express the relationship between the densities of the two liquids:
ρB=2ρc
Since we found earlier that ρc=ρA, we can substitute:
ρB=2ρA
Step 4: Find the ratio of densities
To find the ratio of the densities of the two liquids, we have:
ρAρB=ρA2ρA=12
Final Answer
The ratio of the densities of the two liquids A and B is:
ρAρB=12
When the cube is completely immersed in Liquid A, the buoyant force acting on it is equal to its weight.
W=Density of the cube×Volume of the cube×g
Since the cube is made of a uniform material, we can denote its density as ρc and its volume V as:
V=side3=4cm×4cm×4cm=64cm3
Thus, the weight of the cube is:
W=ρc×64cm3×g
FbA=ρA×V×g=ρA×64cm3×g
Setting the weight equal to the buoyant force gives us:
ρc×64g=ρA×64g
From this, we can simplify to:
ρc=ρA
When the cube is placed in Liquid B, it floats with 2 cm of its height above the liquid. This means that 2 cm of the cube is above the surface, and the remaining part is submerged.
Height submerged=Total height−Height above liquid=4cm−2cm=2cm
The volume submerged is:
V′=side2×height submerged=4cm×4cm×2cm=32cm3
FbB=ρB×V′×g=ρB×32cm3×g
ρc×64g=ρB×32g
From this, we can simplify to:
ρc×64=ρB×32
Now we can express the relationship between the densities of the two liquids:
ρB=2ρc
Since we found earlier that ρc=ρA, we can substitute:
ρB=2ρA
To find the ratio of the densities of the two liquids, we have:
ρAρB=ρA2ρA=12
The ratio of the densities of the two liquids A and B is:
ρAρB=12
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS ( FROM VISCOSITY , STOKES LAW)17videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - VERY SHORT ANSWER QUESTIONS8videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)21videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
Similar Questions
A solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
View SolutionA solid floats in a liquid at 20∘C with 75 % of it immersed. When the liquid is heated to 100∘C, the same solid floats with 80% of it immersed in the liquid. Calculate the coefficient of expansion of the liquid. Assume the volume of the solid to be constant.
View SolutionA certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View SolutionA closed box of thin aluminium foil of volume 10 cc and mass 3 gm is completely filled with a liquid . It is now put into water and when it floats . It is just completely immersed . Find the density of the liquid filled inside the box ( density of water 103kg/m3)
 View Solution
View SolutionA piece of stone of mass 15.1 g is first immersed in a liquid and it weighs 10.9 gf. Then on immersing the piece of stone in water, it weighs 9.7 gf. Calculate the relative density of the liquid.
View SolutionA body is volume 100cm3 weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8×103kgm−3. Find (i) the upthrust due to liquid and (ii) the weight of the body in liquid.
View SolutionA simple pendulum oscillating in air has period T. The bob of the pendulum is completely immersed in a non-viscours liquid. The density of the liquid is 116th of the material of the bob. If the bob is inside liquid all the time, its period of scillation in this liquid is :
View SolutionThe pressures of the gas filled in the bulb of a constant volume gas thermometer are 66 cm and 88 cm of mercury column at 0∘C and 100∘C respectively. When its bulb is immersed in a liquid placed in a vessel, its pressure is 82.5 cm of mercury column. Calculate the temperature of the liquid.
View Solution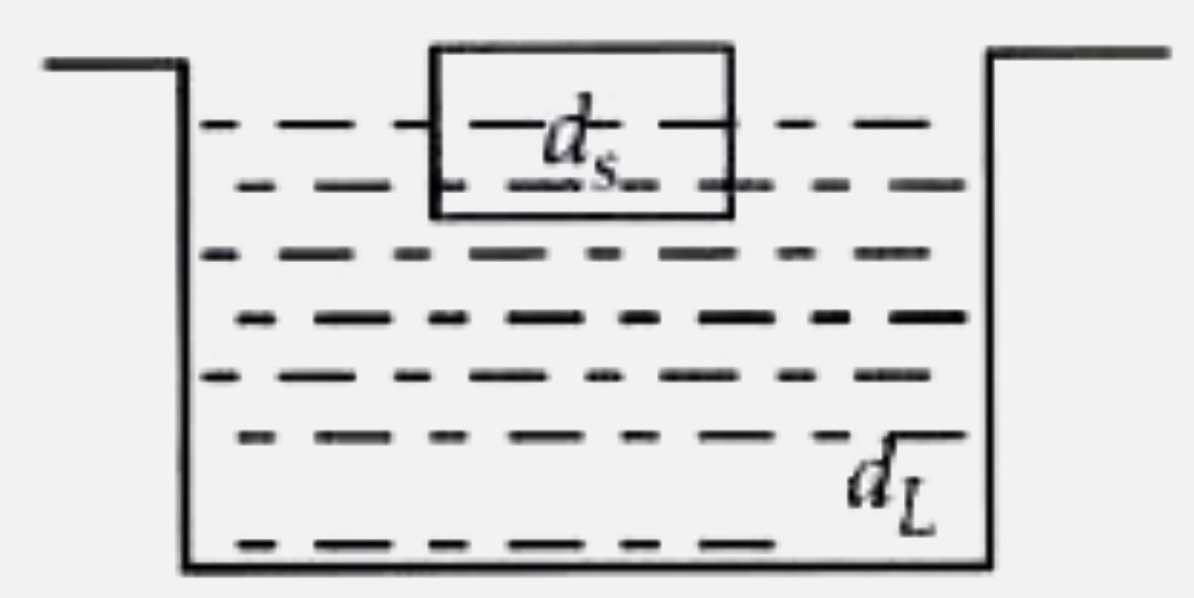
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View Solution

