A tank, with a square base of area 1.0m2 is divided by a vertical partition has a small hinged door of aren 20cm2. The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to the height of 4.0 m. Compute the force necessary to keep the door closed
The correct Answer is:54.88N
To solve the problem of finding the force necessary to keep the door closed in the tank, we will follow these steps:
Step 1: Understand the Problem
We have a tank divided into two compartments. One side contains water and the other contains an acid with a relative density of 1.7. The door between the two compartments has a specific area, and we need to calculate the force required to keep this door closed due to the pressure difference caused by the fluids.
Step 2: Identify the Given Data
- Area of the door, A=20cm2=20×10−4m2=0.002m2
- Height of the fluid column, h=4.0m
- Density of water, ρ1=1000kg/m3
- Relative density of acid = 1.7, thus:
ρ2=1.7×ρwater=1.7×1000kg/m3=1700kg/m3
Step 3: Calculate the Pressure at the Door
The pressure at a depth in a fluid is given by the formula:
P=h⋅ρ⋅g
where g (acceleration due to gravity) is approximately 9.8m/s2.
Pressure on the Water Side (P1):
P1=h⋅ρ1⋅g=4.0m⋅1000kg/m3⋅9.8m/s2=39200Pa
Pressure on the Acid Side (P2):
P2=h⋅ρ2⋅g=4.0m⋅1700kg/m3⋅9.8m/s2=67040Pa
Step 4: Calculate the Pressure Difference
The pressure difference ΔP across the door is given by:
ΔP=P2−P1=67040Pa−39200Pa=27840Pa
Step 5: Calculate the Force
The force F required to keep the door closed can be calculated using the formula:
F=ΔP⋅A
Substituting the values we have:
F=27840Pa⋅0.002m2=55.68N
Final Answer
The force necessary to keep the door closed is approximately 55.68N.
---
We have a tank divided into two compartments. One side contains water and the other contains an acid with a relative density of 1.7. The door between the two compartments has a specific area, and we need to calculate the force required to keep this door closed due to the pressure difference caused by the fluids.
- Area of the door, A=20cm2=20×10−4m2=0.002m2
- Height of the fluid column, h=4.0m
- Density of water, ρ1=1000kg/m3
- Relative density of acid = 1.7, thus:
ρ2=1.7×ρwater=1.7×1000kg/m3=1700kg/m3
The pressure at a depth in a fluid is given by the formula:
P=h⋅ρ⋅g
where g (acceleration due to gravity) is approximately 9.8m/s2.
P1=h⋅ρ1⋅g=4.0m⋅1000kg/m3⋅9.8m/s2=39200Pa
P2=h⋅ρ2⋅g=4.0m⋅1700kg/m3⋅9.8m/s2=67040Pa
The pressure difference ΔP across the door is given by:
ΔP=P2−P1=67040Pa−39200Pa=27840Pa
The force F required to keep the door closed can be calculated using the formula:
F=ΔP⋅A
Substituting the values we have:
F=27840Pa⋅0.002m2=55.68N
The force necessary to keep the door closed is approximately 55.68N.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS ( FROM VISCOSITY , STOKES LAW)17videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - VERY SHORT ANSWER QUESTIONS8videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)21videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
Similar Questions
A tank with a square base of area 1.0m2 is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm2. The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m. Compute to force necessary the force nec cessary to keep the door closed.
View SolutionA rectangular tank of base area 100 m2 has a height of 2 m. Calculate the thrust at the bottom of the tank, if it is filled upto the brim with water of density 103 kg m−3.
View Solution
Knowledge Check
- Question 1 - Select One
A tank with a square base of area 2m2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20cm2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Takeg=10ms−2)
A10NB20 NC40 ND80 N
A tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
The total force exerted by all the fluids on the conical cork in the vertical direction is
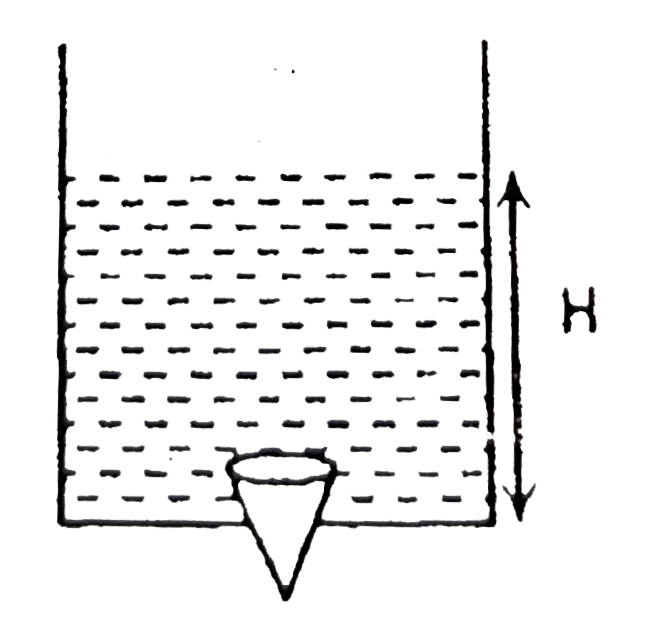 View Solution
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the force exerted by water on the curved surface of the conical cork submerged in water when the liquid level in the vessel is equal to H.
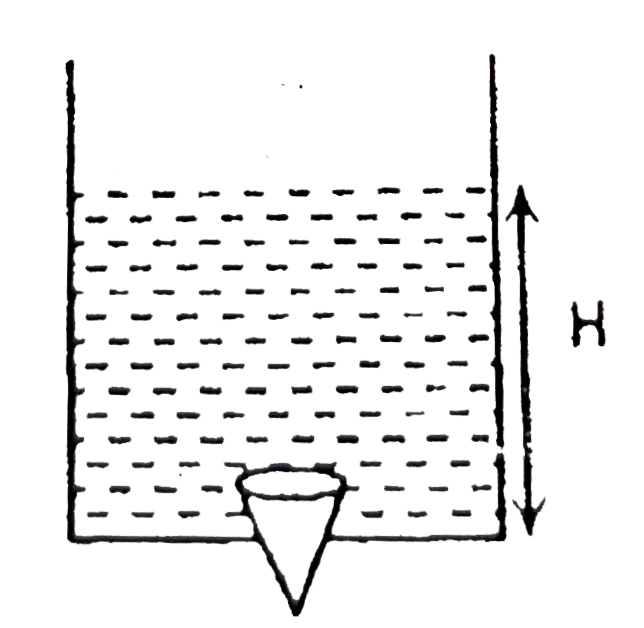 View Solution
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the value of H.
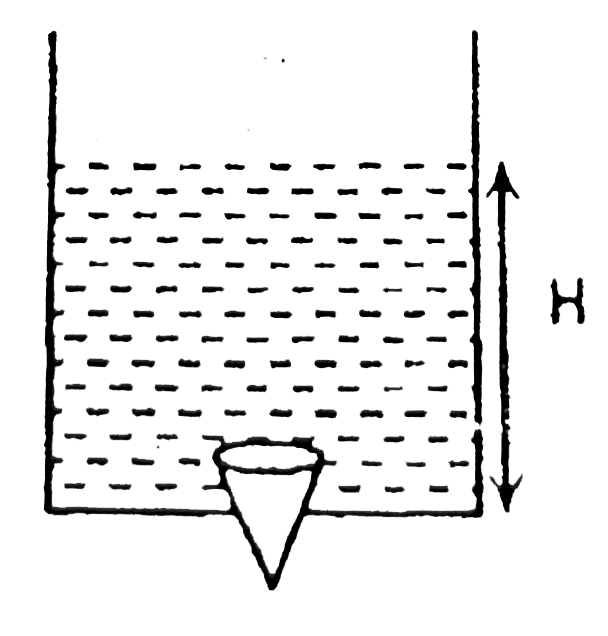 View Solution
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,View Solution
,View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
 View Solution
View Solution

