An iron plate 10−5m2 area, 4×10−3 m thick has its opposite faces maintained at 373 K and 223 K respectively. How much heat flows through the plate per second ? Thermal conductivity of iron =80Wm−1K−1.
The correct Answer is:10 J
To solve the problem of how much heat flows through the iron plate per second, we can use the formula for heat transfer through conduction, which is given by:
Q=k⋅A⋅(T1−T2)⋅tx
Where:
- Q = heat transferred (in Joules)
- k = thermal conductivity (in W/m·K)
- A = area (in m²)
- T1 = temperature of one face (in K)
- T2 = temperature of the opposite face (in K)
- t = time (in seconds)
- x = thickness of the plate (in m)
Step 1: Write down the given values
- Area, A=10−5m2
- Thickness, x=4×10−3m
- Temperature of one face, T1=373K
- Temperature of the opposite face, T2=223K
- Thermal conductivity of iron, k=80W/m⋅K
- Time, t=1s
Step 2: Calculate the temperature difference
Calculate the temperature difference (T1−T2):
T1−T2=373K−223K=150K
Step 3: Substitute the values into the formula
Now substitute the values into the heat transfer formula:
Q=80W/m⋅K⋅10−5m2⋅150K⋅1s4×10−3m
Step 4: Simplify the equation
Now simplify the equation step by step:
1. Calculate the numerator:
80⋅10−5⋅150⋅1=1200⋅10−5=1.2×10−3W⋅s
2. Divide by the thickness:
Q=1.2×10−34×10−3=0.3J/s
Step 5: Final answer
Thus, the amount of heat flowing through the plate per second is:
Q=30J
- Q = heat transferred (in Joules)
- k = thermal conductivity (in W/m·K)
- A = area (in m²)
- T1 = temperature of one face (in K)
- T2 = temperature of the opposite face (in K)
- t = time (in seconds)
- x = thickness of the plate (in m)
- Area, A=10−5m2
- Thickness, x=4×10−3m
- Temperature of one face, T1=373K
- Temperature of the opposite face, T2=223K
- Thermal conductivity of iron, k=80W/m⋅K
- Time, t=1s
Calculate the temperature difference (T1−T2):
T1−T2=373K−223K=150K
Now substitute the values into the heat transfer formula:
Q=80W/m⋅K⋅10−5m2⋅150K⋅1s4×10−3m
Now simplify the equation step by step:
1. Calculate the numerator:
80⋅10−5⋅150⋅1=1200⋅10−5=1.2×10−3W⋅s
2. Divide by the thickness:
Q=1.2×10−34×10−3=0.3J/s
Thus, the amount of heat flowing through the plate per second is:
Q=30J
Topper's Solved these Questions
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM MASS OF ICE MELTED
Explore 17 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
Explore 3 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:VERY SHORT ANSWER QUESTIONS
Explore 5 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- THERMAL RADIATION Book:ICSEChapter:THERMAL RADIATION Exercise:SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
Explore 14 Videos
Similar Questions
One face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivity of copper is 385Wm−1C−1.
View SolutionThe temperature difference between the ends of a rod of aluminium of length 1.0 m and area of cross section 5.0 cm2 is 200∘C. How much heat will flow through the rod in 5 minutes ? The coefficient of thermal conductivity of aluminium is 0.2 kJ s−1 m−1 ∘C−1.
View SolutionFind the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionAn iron boiler is 1 cm thick and has a heating area 2.5m2. The two surface of the boiler are at 230∘C and 100∘C respectively. If the latent heat of the steam is 540kcalkg−1 and thermal conductivity of iron is 1.6×10−2Kcals−1m−1K−1, then how much water will be evaporated into steam per minute ?
View SolutionThe area of a glass window is 1.2m2. The thickness of the glass is 2.2 mm. If the temperature outside is 36°C and the temperature inside is 26°, calculate the heat flowing into the room every hour. Thermal conductivity of glass is 0.8Wm−1K−1.
View SolutionCalculate the rate of loss from a room through a glass window of area 1.5m2 and thickness 2.5×10−3 m, when the temperature of the room is 25∘C and that of the air outside is 10∘C. Assume that the inner glass surface is at the room temperature. [ Thermal conductivity of glass =1.2Wm−1K−1 ]
View SolutionA brass boiler has a base area of 0.15m2 and thickness is 1.0cm. It boils water at the rate of 6.0kg/min. When placed on a gas stove. Estimate the temperature of the part of the flame in contact. With the boiler. Thermal conductivity of brass =109Wm−1K−1
View SolutionTwo parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are 4.0cm and 2.5cm respectively and the area of cross section is 100cm2 for each plate. The thermal conductivities are KA=200Wm−1C−1 for plate A and KB=400Wm−1C−1 for the plate B. The outer surface of the plate A is maintained at100∘C and the outer surface of the plate B is maintained at 0∘C. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.

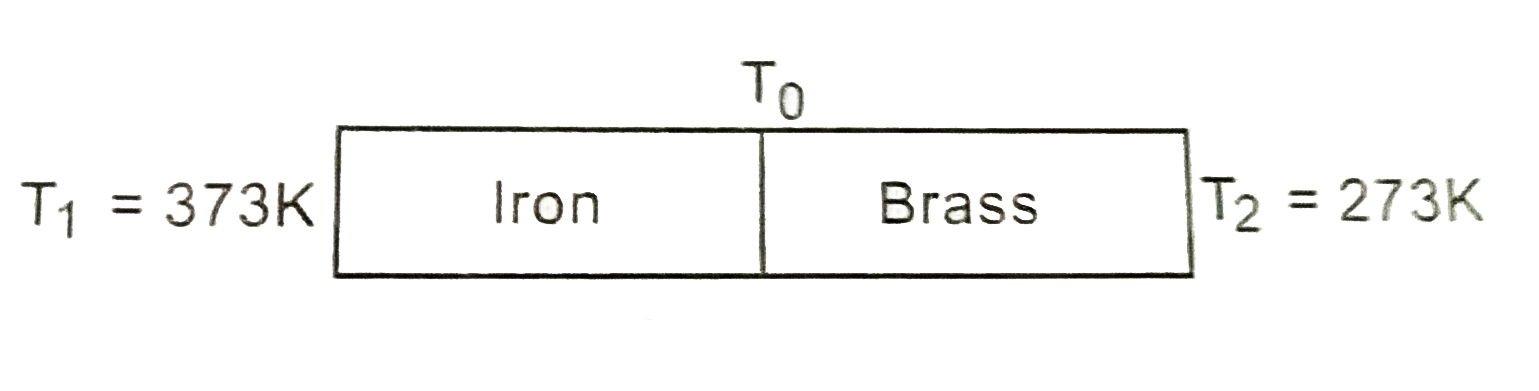
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View Solution