Three rods AB, BC and CD are connected as shown is Fig.11.23. They are of the same length and area of cross-section. The thermal resistance of AB is 15KW−1,BC is 10KW−1 an CD is 15KW−1. If the free ends are maintained at 100∘Cand0∘C, calculate the rate of heat flowing through the combination.

The correct Answer is:2.5W
Q/t=θ1−θ2/R1+R2+R3=100−0/15+10+15=2.5 W
Topper's Solved these Questions
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
2 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
3 Videos
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D
6 Videos
- THERMAL RADIATION BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
14 Videos
Similar Questions
A steel frame (K=45Wm−1C−1) of total length 60cm and cross sectional area 0.2cm2 , Forms three side of a square. The free ends are maintained at 20∘C and 40∘C . Find the rate of heat flow through a cross section of the frame.
View SolutionTwo rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

View Solution
Knowledge Check
Two rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
 A50∘CB40∘CC60∘D80∘C
A50∘CB40∘CC60∘D80∘C
A steel farme (K=45Wm−1^(@)C^(-1)of→tal≤n>h60cmandcrosssectionarea0.02cm^(2),Formsthreesofa□.Theeeendsarema∫a∈edat20^(@)Cand40^(@)C . Find the rate of heat flow through a cross section of the frame.
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View SolutionA rod CD of thermal resistance 5.0KW−1isjo∈edatthem≤ofannticalrodABasshown∈figure.TheendsA,BandDarema∫a∈edat100^(@)C,0(@)C and 25(@)C respectively. Find the heat current in CD.
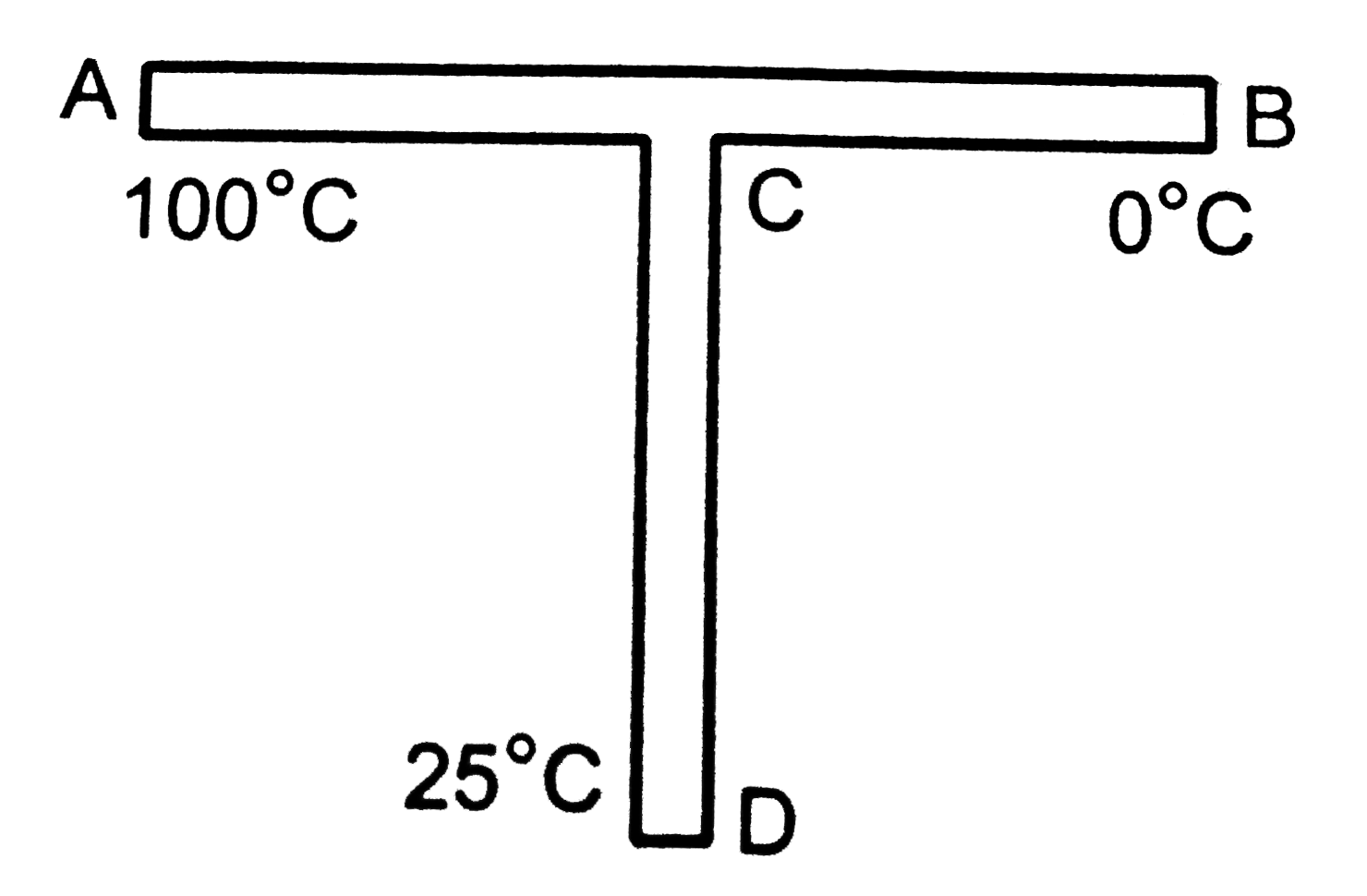
View SolutionA rod CD of thermal resistance 5.0KW−1 is joined at the middle of an identical rod AB as shown in figure. The ends A, B and D are maintained at 100∘C , 0∘C and 25∘C respectively. Find the heat current in CD.

View SolutionA rod CD of thermal resistance 5.0KW−1 is joined at the middle of an identical rod AB as shown in figure. The ends A,B and D are maintained at 100∘C , 0∘C and 25∘C respectively. Find the heat current in CD.

View Solution(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionThree rods of lengths 20cm each and area of cross section 1cm2 are joined to from a triangle ABC. The conductivities of the rods are kAB=50Js−1m−1C−1 , kBC=200Js−1m−1C−1 , and kAC=400Js−1m−1C−1 . The junction A,B and C are maintained at 40∘C , 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB, AC and BC .
View Solution
