Question

State Stefan's law and Wien's displacement law. Draw graphs showing the distribution of energy in the spectrum of a black body. Explain what quantity is plotted against the wavelength . By considering how this energy distribution varies with tempaerature expalin the colour changes which occur when a piece of iron is heated from cold to near the melting point.

Explanation

Step-by-Step Solution

Step 1: State Stefan's Law

Stefan's Law, also known as Stefan-Boltzmann Law, states that the total energy radiated per unit surface area of a black body is directly proportional to the fourth power of its absolute temperature (T). Mathematically, it can be expressed as:

\( E = \sigma T^4 \)

where:
- \( E \) is the total energy radiated per unit area,
- \( \sigma \) is the Stefan-Boltzmann constant (\( 5.67 \times 10^{-8} \, \text{W/m}^2 \text{K}^4 \)),
- \( T \) is the absolute temperature in Kelvin.

Step 2: State Wien's Displacement Law

Wien's Displacement Law states that the wavelength (\( \lambda_{max} \)) at which the emission of a black body spectrum is maximized is inversely proportional to the absolute temperature (T) of the black body. This can be mathematically expressed as:

\( \lambda_{max} = \frac{b}{T} \)

where:
- \( \lambda_{max} \) is the wavelength at which the emission is maximum,
- \( b \) is Wien's displacement constant (\( 2.898 \times 10^{-3} \, \text{m K} \)),
- \( T \) is the absolute temperature in Kelvin.

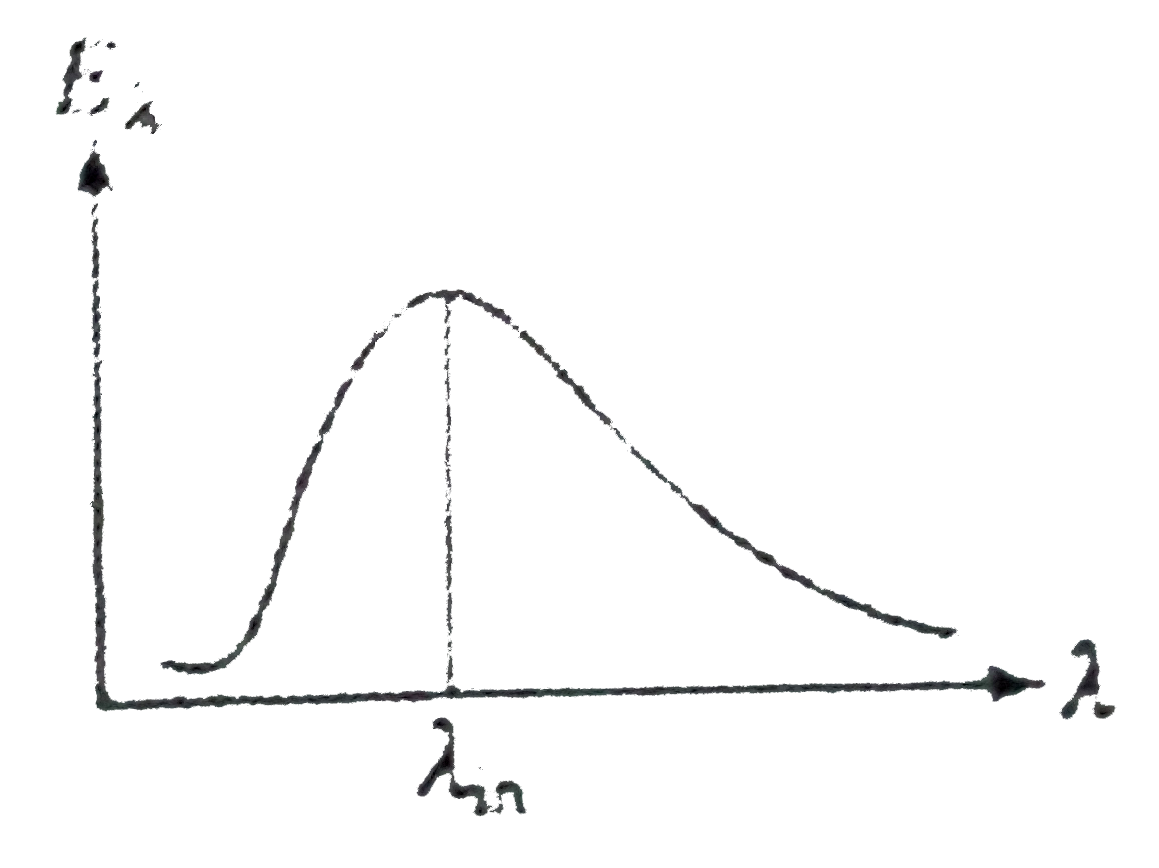
Step 3: Draw Graphs Showing the Distribution of Energy in the Spectrum of a Black Body

The graph of the black body radiation spectrum typically shows intensity (or energy emitted per unit wavelength) on the y-axis and wavelength on the x-axis. The curve peaks at a certain wavelength that shifts to shorter wavelengths as the temperature increases.

1. At Low Temperature: The peak is at longer wavelengths (infrared region).
2. At Higher Temperature: The peak shifts to shorter wavelengths (visible region).

Step 4: Explain the Quantity Plotted Against Wavelength

In the graph, the quantity plotted against the wavelength is the spectral radiance or intensity of radiation emitted by the black body at different wavelengths. This represents how much energy is emitted at each wavelength.

Step 5: Explain Color Changes When Heating Iron

When a piece of iron is heated from cold to near its melting point, the following color changes occur:

1. At Low Temperatures: The iron appears dull red or dark, as it emits mostly in the infrared spectrum (not visible).
2. As Temperature Increases: The iron starts to glow red, indicating that it is emitting visible light due to the increase in temperature. This corresponds to the peak of the emission spectrum moving into the visible range.
3. At Higher Temperatures: As the temperature approaches the melting point, the color changes to bright orange and then to yellow. This is due to the peak of the emission spectrum shifting further into the visible spectrum (shorter wavelengths).
4. Near Melting Point: The iron may appear white-hot, indicating that it emits a broad spectrum of visible light.

This color change can be explained by Wien's Displacement Law, which shows that as the temperature increases, the peak wavelength of emitted radiation decreases, leading to a shift from infrared to visible light.