Figures below show four different spring arrangements. If the mass in each arrangement is displaced from its equilibrium position and released, what is the resulting frequency of vibration in each case ? Neglect the mass of the each spring. (See Fig).

Fig.(a) and (b) represents springs in parallel.
Let x be the extension produced in each spring. The total restoring force is mm F. Let k1andk2 be the spring constants
F=−k1x−k2x
=−(k1+k2)x=−kx
where k=k1+k2
The period of oscillation
T=2π√mk
=2π√mk1+k2
Fig (c) and (d) represent springs in series

Let x1andx2 be the extension in the the two springs. The restoring force acting in the two spring is the same. [Note Instead of x1 & x2,y1&y2 could also be used]
So F=−k1x1=−k2x2
x1=−Fk1,x2=−Fk2
Total extension x=x1+x2
=−Fk1−Fk2=−F[1k1+1k2]
=−F[k2+k1k2k1]
F=−(k1k2k1+k2)x=−kx
where k=k1k2k1+k2
Period of oscillation =T=2π√mk=2π√m(k1+k2)k1k2
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS WITH ANSWER
20 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Figure-1 to Figure -4 shows four different spring arrangements . Mass m in each arrangement is displacement from its equilibrium position and released Neglec mass of the springs. Choose the correct statement (s)

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA cart of mass 2.00kg is attached to the end of a horizontal spring with force constant k=150N/m. The cart is displaced 15.0cm from its equilibrium position and released. What are
(a) the amplitude (b) the period ( c) the mechanical energy (e) the maximum velocity of the cart ? Neglect friction.
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
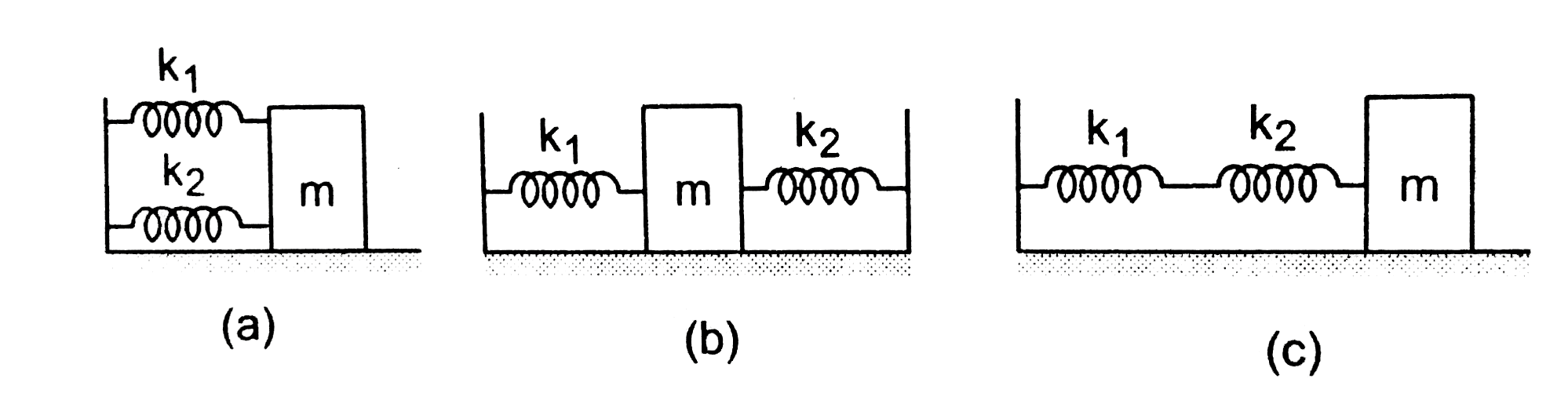
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View Solution
