A trolley of mass 3.0kg is connected to two identical springs each of force constant
600Nm−1as shown in figure 13.32 (amplitude=5cm)
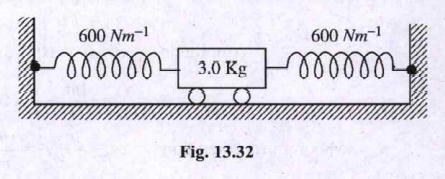
Problem (a) period of oscillation
Problem (b) the max speed of trolley.
If the spring in the problem are replaced by rubber bands, what is the answer to the question (a) and (b) in the problem if K of rubber band is 600Nm−1 during extensions.
Rubber band acts like a spring during stretching only . So there is no restoring force during compression.
(a) ∴T=2π√mk=2x√3600=0.44s
vmax=aω=a√km=0.05√6003=0.71ms−1
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS WITH ANSWER
20 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
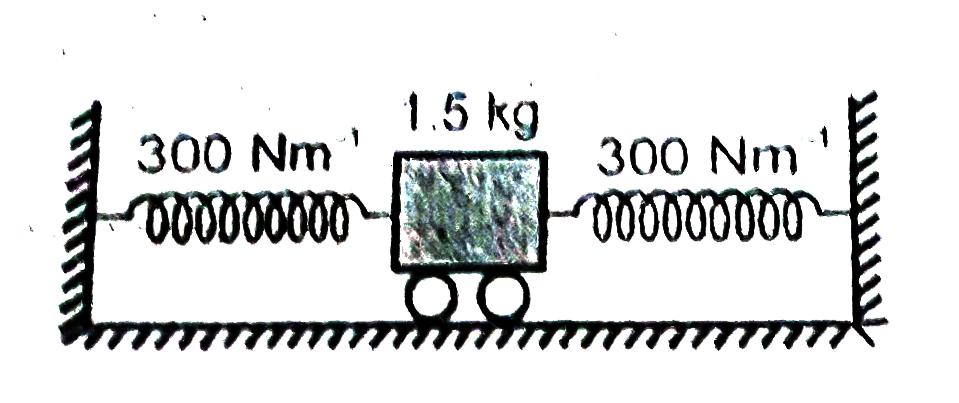
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
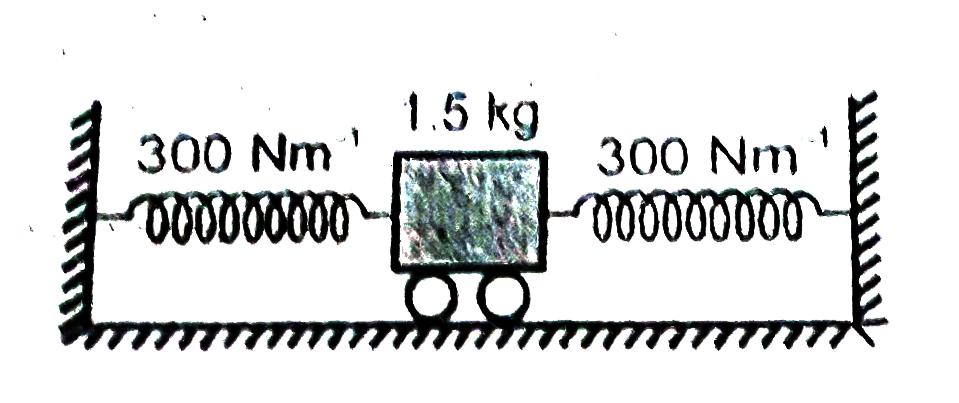
View Solution
Knowledge Check
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
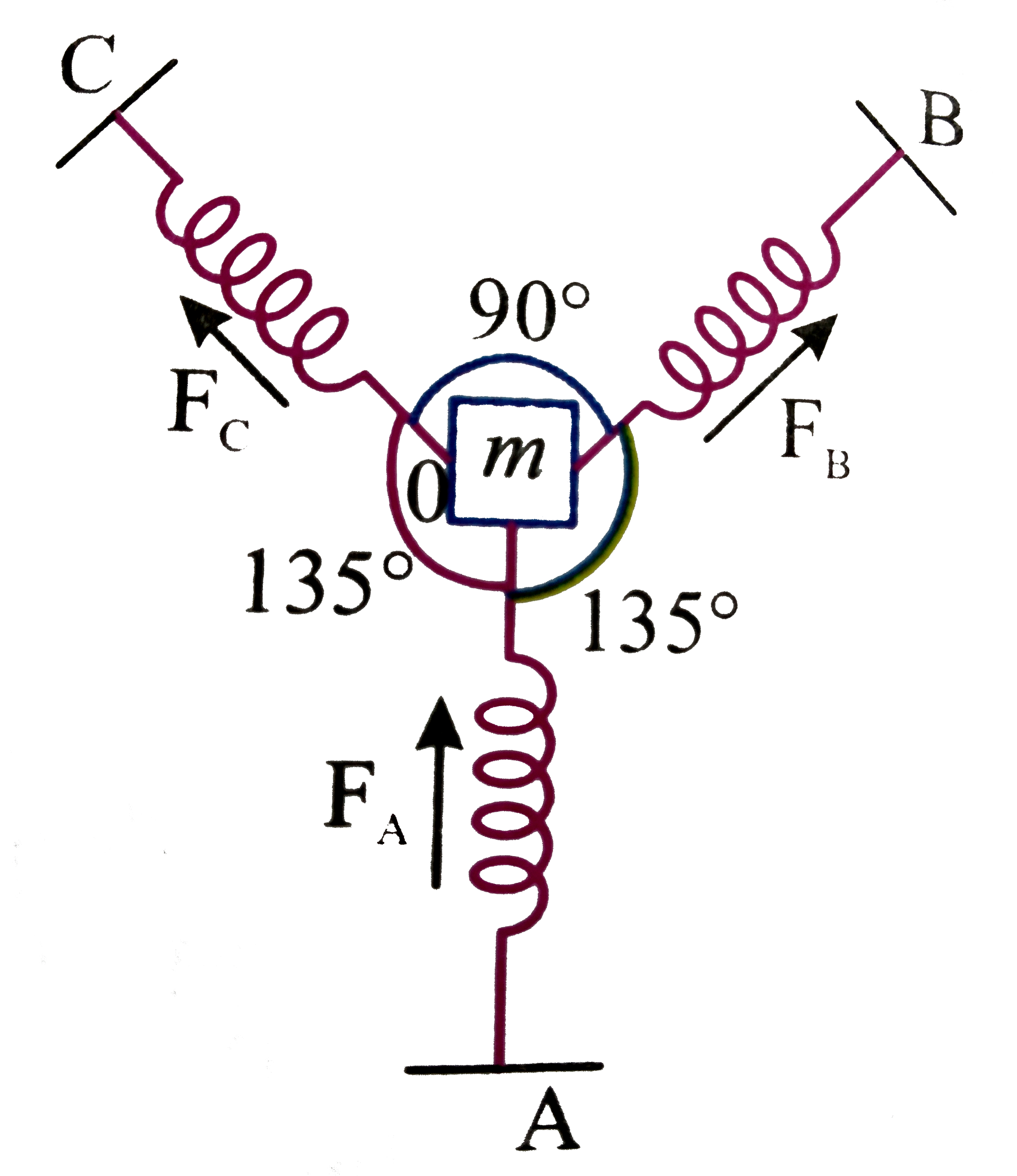 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
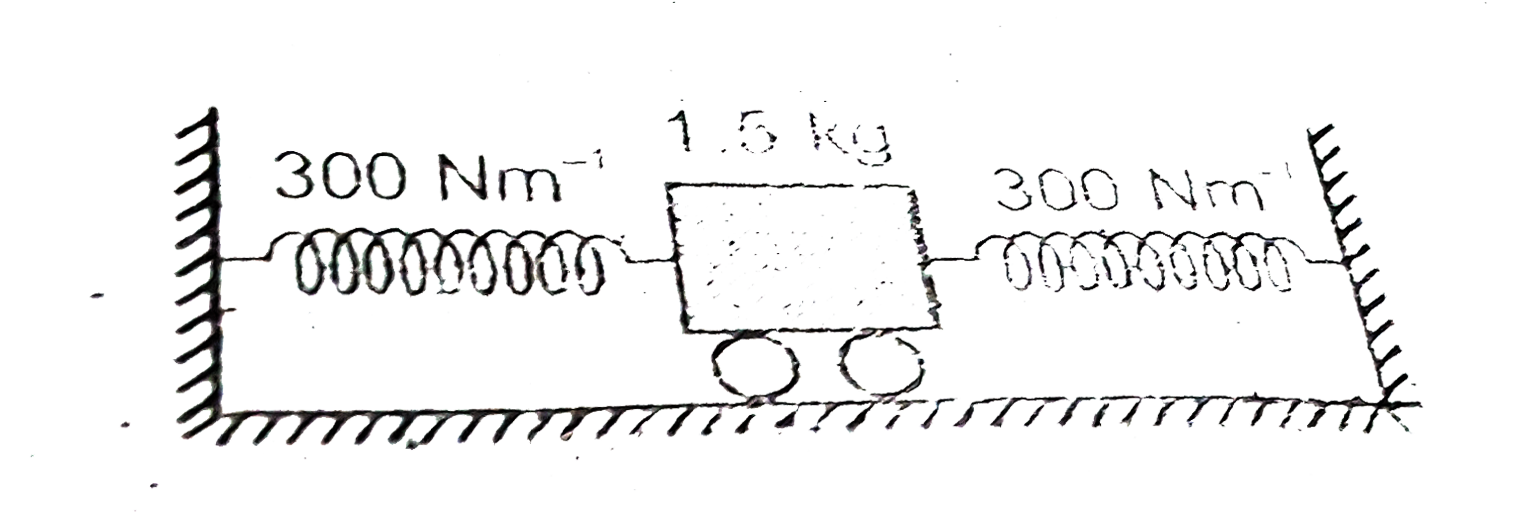
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
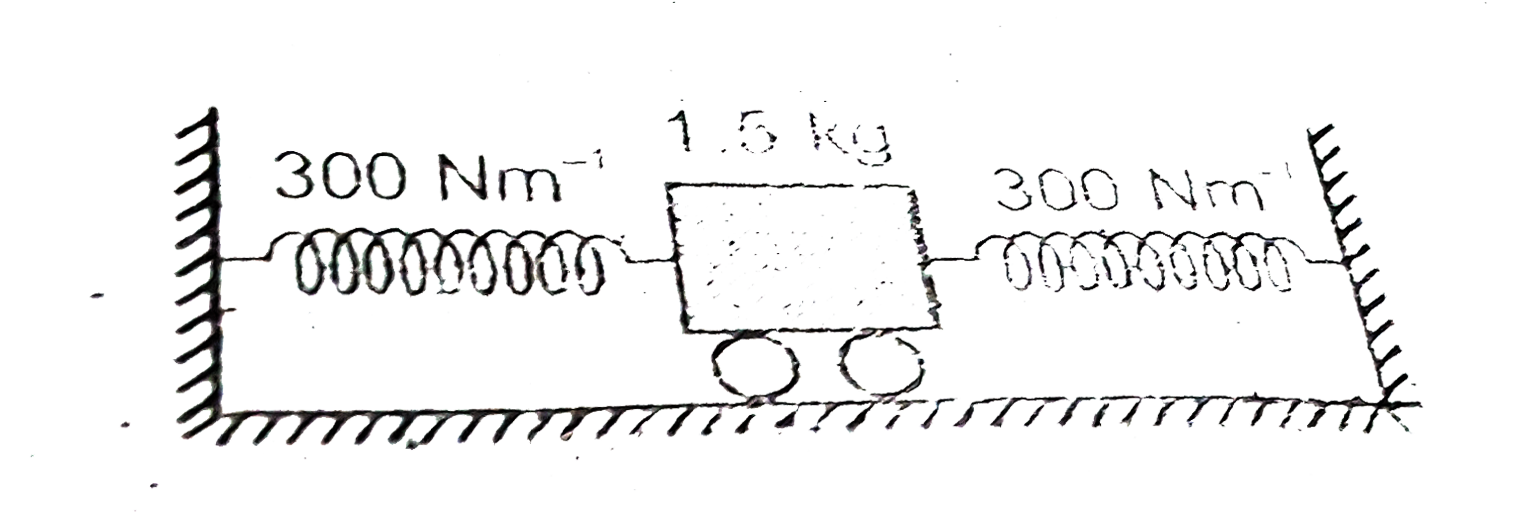
View SolutionA trolley of mass 3.0 kg is connected to two identical rubber bands each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from an equilibrium position by 5.0 cm and released, what is the period of ensuing oscillations?

View SolutionA trolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View SolutionA tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View SolutionProblem Based on Spring
View Solution
