A small trolley of mass 2.0 kg resting on a horizontal turntable is connected by a light spring to the centre of the table. When the turntable is set into rotation at a speed of 300 rev/min the length of the stretched spring is 40 cm. If the original length of the spring is 35 cm, determine the force constant of the spring.
The correct Answer is:15775.36Nm−1
To solve the problem, we need to determine the force constant (k) of the spring when a small trolley of mass 2.0 kg is rotating on a turntable. Here are the steps to find the solution:
Step 1: Convert the rotational speed from revolutions per minute to radians per second.
The given speed is 300 revolutions per minute (rev/min). We can convert this to radians per second (rad/s) using the following conversion factors:
Angular speed(ω)=speed in rev/min×2π rad1 rev×1 min60 s
Calculating this gives:
ω=300×2π60=10π rad/s
Step 2: Determine the extension of the spring.
The original length of the spring is 35 cm, and the length of the stretched spring is 40 cm. The extension (x) of the spring can be calculated as:
x=stretched length−original length=40 cm−35 cm=5 cm=0.05 m
Step 3: Use the centripetal force equation.
When the trolley rotates, the centripetal force required to keep it moving in a circle is provided by the spring force. The centripetal force (F_c) can be expressed as:
Fc=m⋅r⋅ω2
Where:
- m = mass of the trolley = 2.0 kg
- r = stretched length of the spring = 0.4 m
- ω = angular velocity = 10π rad/s
Calculating the centripetal force:
Fc=2.0⋅0.4⋅(10π)2
Fc=2.0⋅0.4⋅100π2=0.8⋅100π2=80π2 N
Step 4: Relate the spring force to the force constant.
The force exerted by the spring (F_s) is given by Hooke's Law:
Fs=k⋅x
Setting the centripetal force equal to the spring force:
80π2=k⋅0.05
Step 5: Solve for the force constant (k).
Rearranging the equation to solve for k:
k=80π20.05
Calculating k:
k=1600π2 N/m
Using π≈3.14:
k≈1600⋅(3.14)2≈1600⋅9.86≈15776 N/m
Final Answer:
The force constant of the spring is approximately k≈15776 N/m.
---
The given speed is 300 revolutions per minute (rev/min). We can convert this to radians per second (rad/s) using the following conversion factors:
The original length of the spring is 35 cm, and the length of the stretched spring is 40 cm. The extension (x) of the spring can be calculated as:
When the trolley rotates, the centripetal force required to keep it moving in a circle is provided by the spring force. The centripetal force (F_c) can be expressed as:
- m = mass of the trolley = 2.0 kg
- r = stretched length of the spring = 0.4 m
- ω = angular velocity = 10π rad/s
The force exerted by the spring (F_s) is given by Hooke's Law:
Rearranging the equation to solve for k:
The force constant of the spring is approximately k≈15776 N/m.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (PERIOD OF OSCILLATION OF (i) A LIQUID IN A U-TUBE, (ii) TEST TUBE FLOAT, (iii) (iii) A PISTON IN AN ENGINE etc.)
9 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM ENERGY OF AS.H. OSCILLATOR )
9 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View SolutionA spring is kept compressed by a small trolley of mass ring 0-5 kg lying on a smooth horizontal surface as shown in the adjacent Fig. When the trolley is released, it is found to move at a speed = 2 m s−1. What potential energy did the spring poses when compressed?

View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table and a mass of 3.0 kg of attached to the free and of the spring. The mass is made to rotate with an angular velocity of 10 rad/s. What is the elongation produced in the spring if its unstretched length is 60 cm ?
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

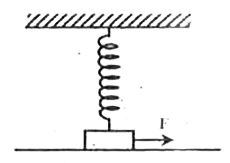
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionA particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring

View Solution
