A spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
Zero
12kx2
32kx2
−12kx2
To solve the problem of finding the work done by the spring force when a spring is stretched by a distance x and then compressed to the same distance, we can follow these steps:
1. Understand the Spring Force and Potential Energy:
The work done by the spring force can be calculated using the change in elastic potential energy of the spring. The formula for the elastic potential energy (PE) stored in a spring is given by:
PE=12kx2
where k is the spring constant and x is the displacement from the equilibrium position.
2. Calculate Potential Energy When Stretched:
When the spring is stretched by a distance x, the potential energy (PE_initial) is:
PEinitial=12kx2
3. Calculate Potential Energy When Compressed:
When the spring is then compressed by the same distance x, the potential energy (PE_final) is:
PEfinal=12kx2
4. Determine the Work Done by the Spring:
The work done by the spring force is the change in potential energy, which can be expressed as:
W=PEfinal−PEinitial
Substituting the values we calculated:
W=(12kx2)−(12kx2)=0
5. Conclusion:
Therefore, the work done by the spring force when it is stretched and then compressed back to the same distance is:
W=0 Joules
Final Answer:
The work done by the spring force is 0 Joules.
The work done by the spring force can be calculated using the change in elastic potential energy of the spring. The formula for the elastic potential energy (PE) stored in a spring is given by:
PE=12kx2
where k is the spring constant and x is the displacement from the equilibrium position.
When the spring is stretched by a distance x, the potential energy (PE_initial) is:
PEinitial=12kx2
When the spring is then compressed by the same distance x, the potential energy (PE_final) is:
PEfinal=12kx2
The work done by the spring force is the change in potential energy, which can be expressed as:
W=PEfinal−PEinitial
Substituting the values we calculated:
W=(12kx2)−(12kx2)=0
Therefore, the work done by the spring force when it is stretched and then compressed back to the same distance is:
W=0 Joules
The work done by the spring force is 0 Joules.
Similar Questions
Work done by a spring force is
View SolutionIn the previous illustration. Consider the situation when the string is completely compressed. Then it begins to relax and will come to its original length.
a. What is the work done by the spring during the period?
b. Is the work done by the spring positive or negative?
View Solution
Knowledge Check
A spring is stretched by applying a load to its free end. The strain produced in the spring is
AvolumetricBshearClongitudinal and shearDlongitudinal.
One end of a fixed spring is pulled by an average force of 10N through a distance of 5cm, find the work done by the spring.
View SolutionA spring is stretched by applying a load to its free end. The strain produced in the spring is
View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionA spring of force constant K is first stretched by distance a from its natural length and then further by distance b. The work done in stretching the part b is
View SolutionTwo masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
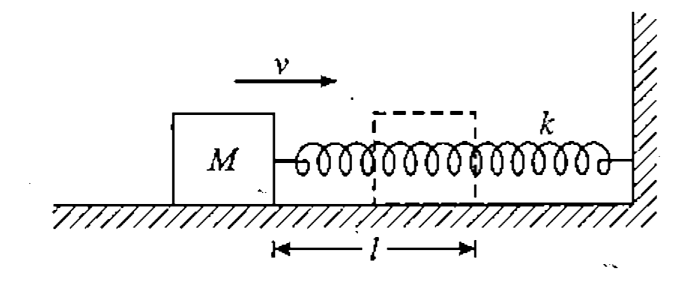
View SolutionThe block of mass M in figure −4.160, initially has a velocity vo to the right and its positionis much that the spring exerts no froce on it, i.e, the spring is not stretched or comkpressed. The block moves to the right a distance l before sttoping in the dotted position shown. The speing constant is k and the coefficeent of kinetic friction between block and table is μ. as the block moves the distance l, (a) what is the work done on it by the friction force ? (b) What is the work done on it by the spring force ? (c) are there other forces actionon the block, and if so what work do they do ? (d) what is the total work done on the block?
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
