Show that CV=Rγ−1
To show that CV=Rγ−1, we can follow these steps:
Step 1: Understand the Definitions
We start with the definitions of the heat capacities:
- CP: Heat capacity at constant pressure
- CV: Heat capacity at constant volume
- R: Universal gas constant
- γ: Ratio of heat capacities defined as γ=CPCV
Step 2: Use the Relationship Between CP and CV
From thermodynamics, we know the relationship:
CP−CV=R(1)
Step 3: Express CP in Terms of CV
Using the definition of γ:
γ=CPCV⟹CP=γCV(2)
Step 4: Substitute CP in Equation (1)
Now, we substitute equation (2) into equation (1):
γCV−CV=R
Step 5: Factor Out CV
We can factor out CV from the left side:
CV(γ−1)=R
Step 6: Solve for CV
Now, we can solve for CV:
CV=Rγ−1
Conclusion
We have shown that:
CV=Rγ−1
We start with the definitions of the heat capacities:
- CP: Heat capacity at constant pressure
- CV: Heat capacity at constant volume
- R: Universal gas constant
- γ: Ratio of heat capacities defined as γ=CPCV
From thermodynamics, we know the relationship:
CP−CV=R(1)
Using the definition of γ:
γ=CPCV⟹CP=γCV(2)
Now, we substitute equation (2) into equation (1):
γCV−CV=R
We can factor out CV from the left side:
CV(γ−1)=R
Now, we can solve for CV:
CV=Rγ−1
We have shown that:
CV=Rγ−1
Topper's Solved these Questions
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - LONG ANSWER QUESTIONS8videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SHORT ANSWER QUESTIONS30videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - ADDITIONAL SOLVED PROBLEMS12videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
Similar Questions
In an isobaric process, ΔQ=Kγγ−1 where γ=CP/CV. What is K?
View SolutionProve that Cp−Cv=R.
View SolutionShow that r1+r2=ccot(C2)
View SolutionLet V and I respresent, respectively, the readings of the voltmeter and ammetre shows in Fig. 6.34, and let RV and RV be their equivalent resistances. Because of the resistances of the meters, the resistnce R is not simply equal to V/I.
(a) When the circuit is connected as shows in Fig. 6.34 (a), shows that R=VI−RA
Explain why the true resistance R is always less than V/I.
(b) When the connections are as shows in Fig.6.34 (b)
Show that R=VI−(V/RV)
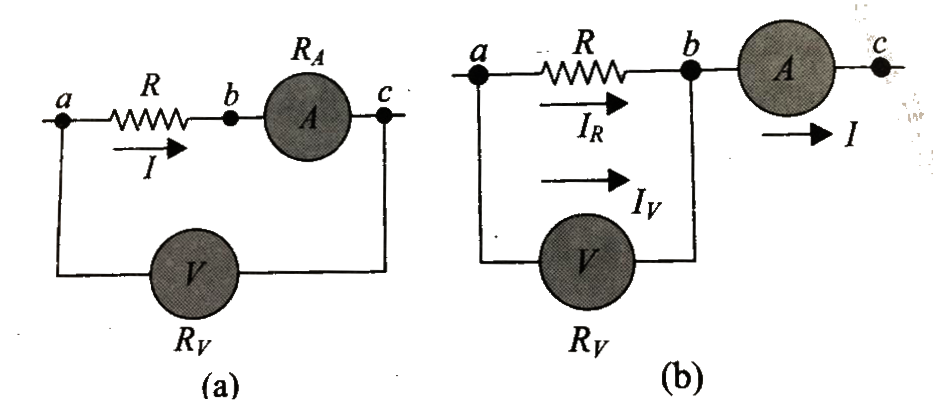
Explain why the true resistance R is always greater than V/I.
(c ) Show that the power delivered to the resistor in part
(i) is IV−I2RA and that in part (ii) is IV−(V2/RV)View SolutionShow that b−cr1+c−ar2+a−br3=0
View SolutionShow that 16R2rr1r2r3=a2b2c2
View SolutionShow that (1r1+1r2)(1r2+1r3)(1r3+1r1)=64R3a2b2c2
View SolutionMolar heat capacity of an ideal gas in the process PVx = constant , is given by : C=Rγ−1+R1−x. An ideal diatomic gas with CV=5R2 occupies a volume V1 at a pressure P1. The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value.
The molar heat capacity of the gas in the given process is :-View SolutionIf a+bi=c+ic−i,a,b,c∈R, show that a2+b2=1andba=2cc2−1
View SolutionIf α,β,γ are the roots ofx3−3x2+3x+7=0 then show that α−1β−1+β−1γ−1+γ−1α−1=3ω where ω is complex cube of unity .
View Solution

