Pure Rolling
Step by step video solution for Pure Rolling by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A rigid bodyI=CMR2 is set into a motion on a rough horizontal surface with a linear speed v0 in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.
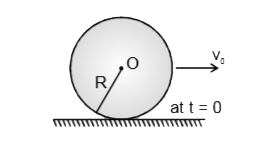
View SolutionA solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution
Knowledge Check
In this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
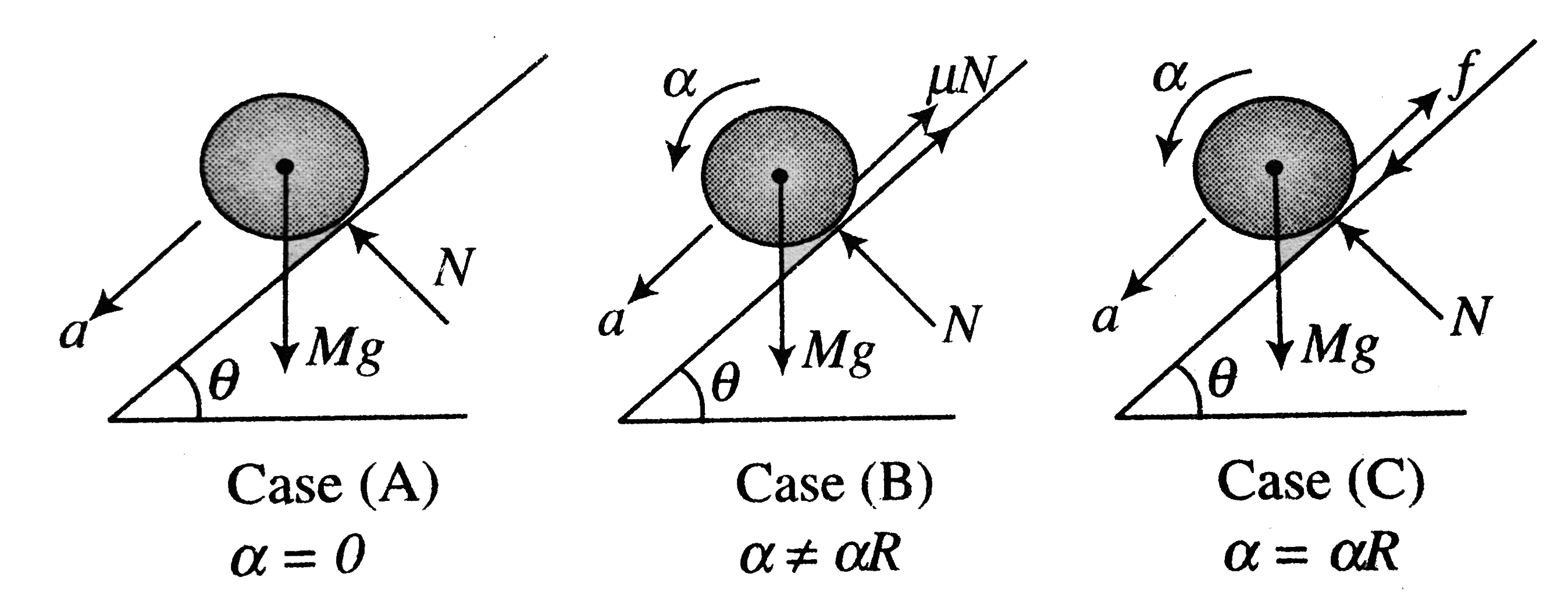
We have four objects: a solid sphere, a hollow sphere, a ring and a disc, all of same radius. When these are released on an inclined plane, it may happen that all of them do not perform pure rolling. But from the information of pure rolling, if one object can be confirmed to be purely rolling then it can be said that rest all will perform pure rolling. This object whose pure rolling confirms pure rolling of all other objects isAhollow sphereBsolid sphereCringDdiscFigure shows a yo-yo placed on a rough surface friction is sufficient for pure rolling. After force F acts pure rolling begins

Statement-1: Angular acceleration of yo-yo is in clockwise sense.
Statement-2: Torque due to F must be larger than the torque due to friction.AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.A ball of radius r is rolling (pure rolling) on a convex stationary circular surface of radius R with angular velocity ω and angular acceleration α. The magnitude of vertical acceleration of top point of the ball is
Aω2r(R+2rR+r)Bω2rCω2rR+rDω2rRR+r
A hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View SolutionIn this passage a brief idea is given of the motion of the rolling bodies on an inclined plane. We will consider three cases: objects are released on an incline plane
Case-A: which is smooth.
Case-B: where friction is insufficient to provide pure rolling.
Case-C: where friction is sufficient to provide pure rolling. Force diagram for three cases are as follows: (where symbols have their usual meanings)
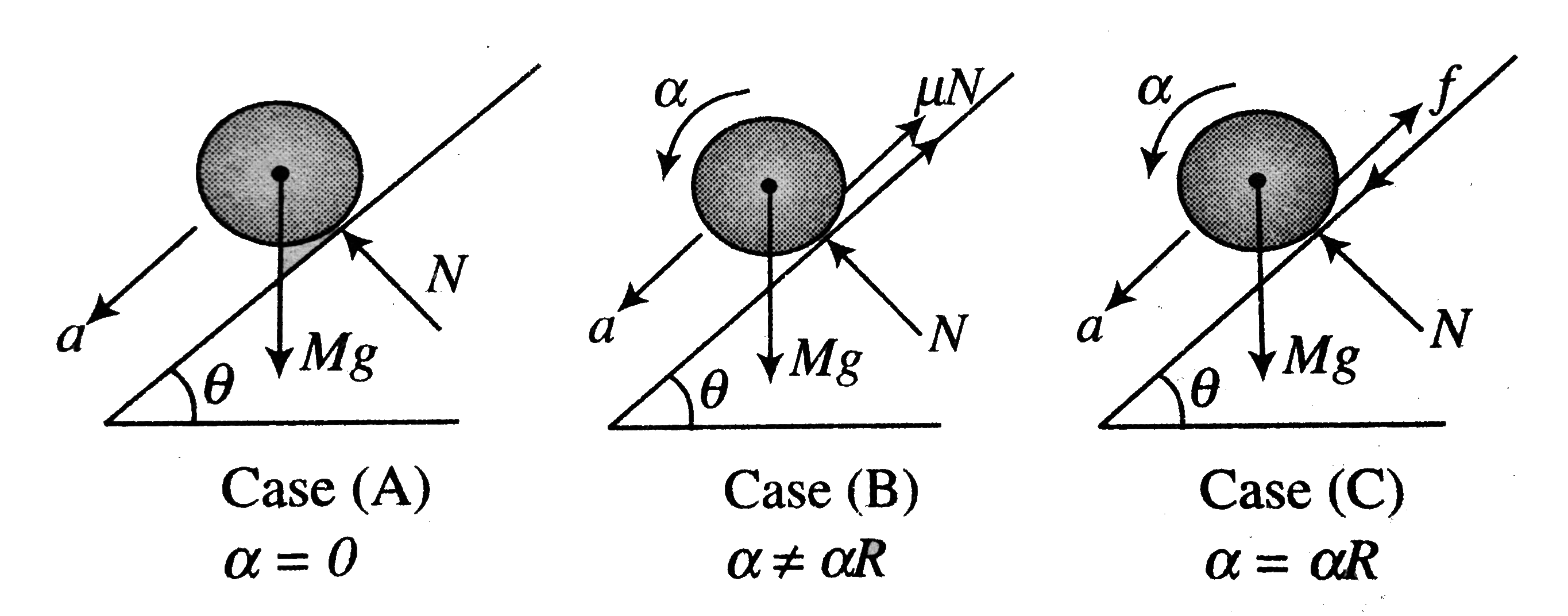
Three solid uniform spheres are released on an inclined plane as shown in the figure. The distance between the spheres remains constant during motion in:

View SolutionSphere in pure accelerated rolling

View SolutionA disc is rolling on a rough horizontal surface. The instantaneous speed of the point of contact during perfect rolling is zero with respect to ground.
The force of friction can help in achieving pure rolling condition.
View SolutionThe motion of a sphere moving on a rough horizontal surface changes from pure sliding (without rolling) to pure rolling (without slipping). In this process, the force of friction
(i) intially acts opposite to the direction of motion and late in the direction of motion
(ii) cause linear retardation
(iii) causes angular acceleration
(iv) stops acting when pure rolling begins
View Solution
