A rigid body $I = C M R^{2}$ is set into a motion on a rough horizontal surface with a linear speed $v_{0}$ in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.

Video Solution

Text Solution

Verified by Experts

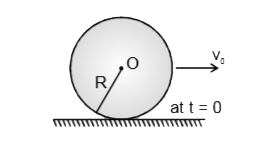
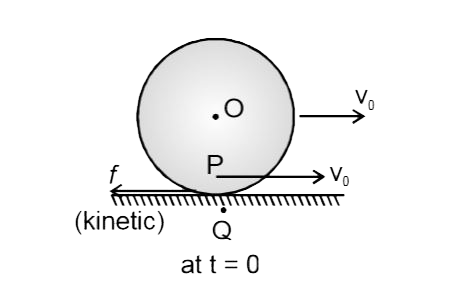
According to the given condition in problem the point P in the body move with speed $v_{0}$ while the point Q on the ground is at rest. So the friciton acts on the body is in backward direction which gives the resultant torque on the body and increase the angualr speed $ω$ as shown in figure.
As shown in above figure initially $v > R ω$ so forward slipping takes place. After introducing the friciton speed decreases and $o m r g a$ increases and at time t = t the relation v = r $ω$ is satisfied. Therefore pure rolling starts. Initially the friciton is kinetic untill the motion is in slipping condition. Afterwards at v = r $ω$ fricition is static. We divide the above problem in two parts.
(1) Translational Motion :
Linear acceleration a = $μ g$
So after time $t, v = v_{0} - μ g t . . . (1)$
(2) Rotational Motion :
From $τ_{net} = I α$
Only friction force is responsible for providing torque. So torque about O is
$f . R = I α$
$μ m g R = C m R^{2} α . . . (2)$
$α$ is angular acceleration of the body
From eq.(2) $α \frac{μ g}{C R}$
$∵ ω = \frac{V}{R}$ at pure rolling condition.
So, $v = \frac{μ g t}{C} . . . (3)$
from eq. (1) & (3)
$\Rightarrow v_{0} - μ g t = \frac{μ g t}{C} \Rightarrow t = \frac{v_{0} C}{μ g (1 + C)} . . . (4)$
Equation (4) gives the time after the pure rolling starts.
Put the value from eq. (4) to eq. (1)
$v = v_{0} - \frac{v_{0} C}{(1 + C)} \Rightarrow v = \frac{v_{0}}{1 + C} . . . (5)$
Equation (5) gives the linear speed at pure rolling situation.
Alternate solution :
Net torque on the body about the bottom most point A is zero. Therefore angular momentum of the body will remain conserved about the bottom most point
Net torque about $A τ_{A} = 0$
$\Rightarrow$ from Angular momentum conservation $L_{i} = L_{f}$
$m v_{0} R = I o m r g a + m v R$
$m v_{0} R = C m R^{2} \frac{v}{R} + m v R$
$v_{0} = C v + v \Rightarrow v = \frac{v_{0}}{1 + C}$

Updated on:21/07/2023