ΔS System and ΔS Surroundings and ΔS Universe for isothermal (RP/IP/free Expansion) || Adiabatic (RP/IP/FE) || Isochoric (RP/IP) || Isobaric (RP/IP)
Step by step video solution for ΔS System and ΔS Surroundings and ΔS Universe for isothermal (RP/IP/free Expansion) || Adiabatic (RP/IP/FE) || Isochoric (RP/IP) || Isobaric (RP/IP) by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023समान प्रश्न
Idea OF Entropy || Second Statement OF SLOT || Calculation OF ΔS System ΔS Surroundings and ΔS Universe for Different -2 Process || Case I :-Change OF State OF IG (ideal Gas)
View SolutionCalculation OF Entropy OF System, Surrounding || Total Entropy for Isochoric Process, Isobaric Process, Isothermal Process, Adiabatic Process
View Solution
ज्ञान जांच
Work is the mode of transference of energy. If the system involves gaseous substance and there is difference of pressure between system and surroundings, such a work is referred to as pressure - volume work (WPV=−PextΔV). It has been observed that reversible work done by the system is the maximum obtainable work. wrev>wirr
The works of isothermal and adiabatic processes are different from each other. for isothermal reversible proces,
Wisothermal reversible=2.303nRTlog10(V2V1)
Wadiabatic reversible=CV(T1−T2)
Calculate work done when 1 mole of an ideal gas is expanded reversibly from 20 L to 40 L at a constant temperature of 300 K.Aw1>w2>w3>w4Bw3>w2>w1>w4Cw3>w2>w4>w1Dw3>w1>w2>w4The pressure-volume of varies thermodynamic process is shown in graphs:
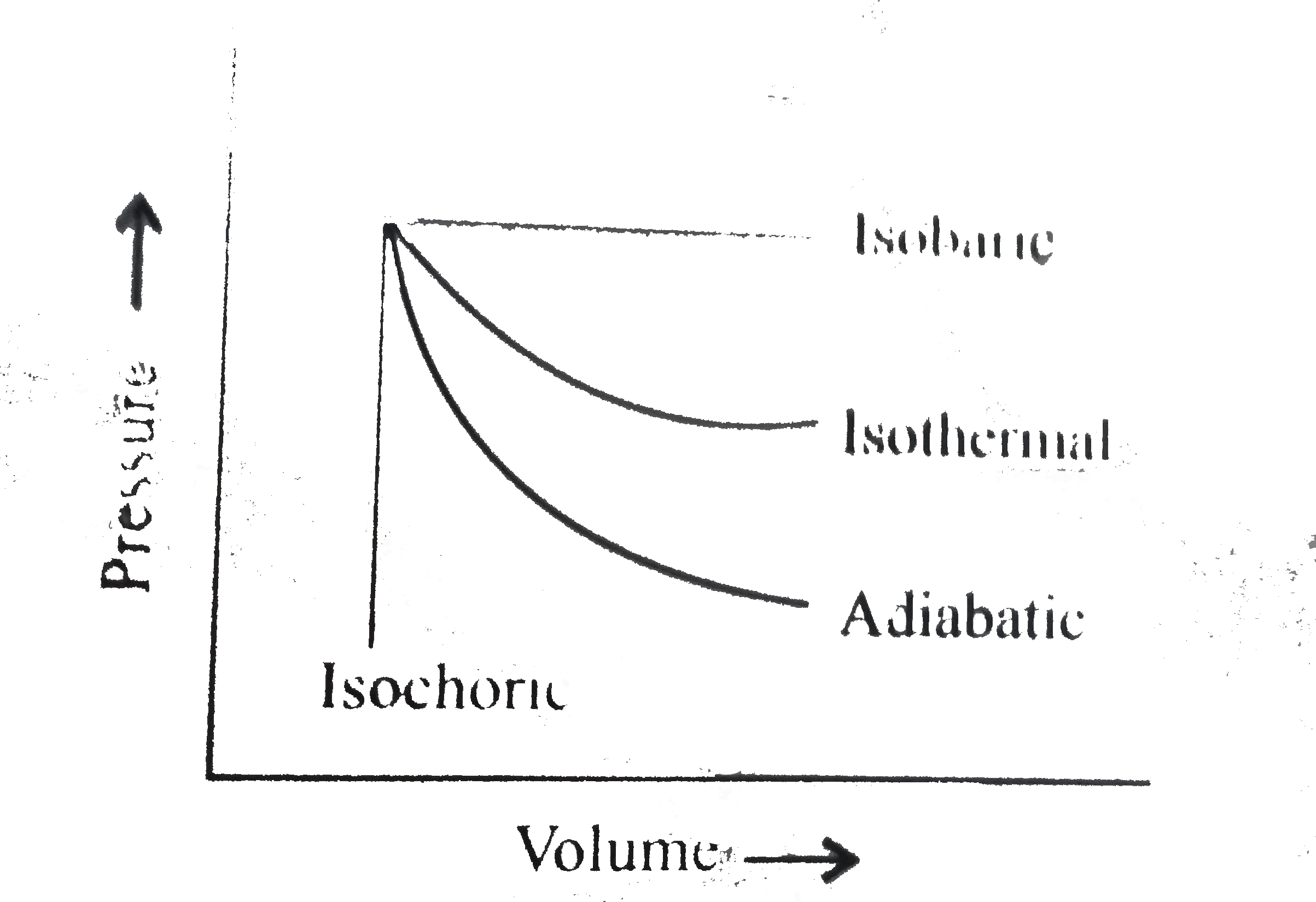
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
If w1,w2,w3 and w4 are work done in isothermal, adiabatic, isobaric, and isochoric reversible processes, respectively then the correct sequence (for expansion) would beAw1<w2<w3<w4Bw3=w2=w1=w4Cw3<w2<w4<w1Dw3>w1>w2>w4DEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the wavelength of photon emitted from an electron jump n=4 to n=2 in a H-like species is 1216Å, then the species is :AH-atomBHe+ ionCLi2+ ionDBe3+ ion
DEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the I excitation potential of a hypothetical H-like is 62 V, then the value of II excitation energy is about :
View SolutionDEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the binding energy of II excitec state of a H-like species is 13.6 eV, then:
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
(i) For a reaction entropy change is given by ΔS=∑S(product)−∑S(reactant)
(ii)ΔS=QrevT=WrevT=nRTln(V2/V1)T
=nRTln(V2)V1=nRln(P1)P2
(iii)ΔS=ΔH−TΔS
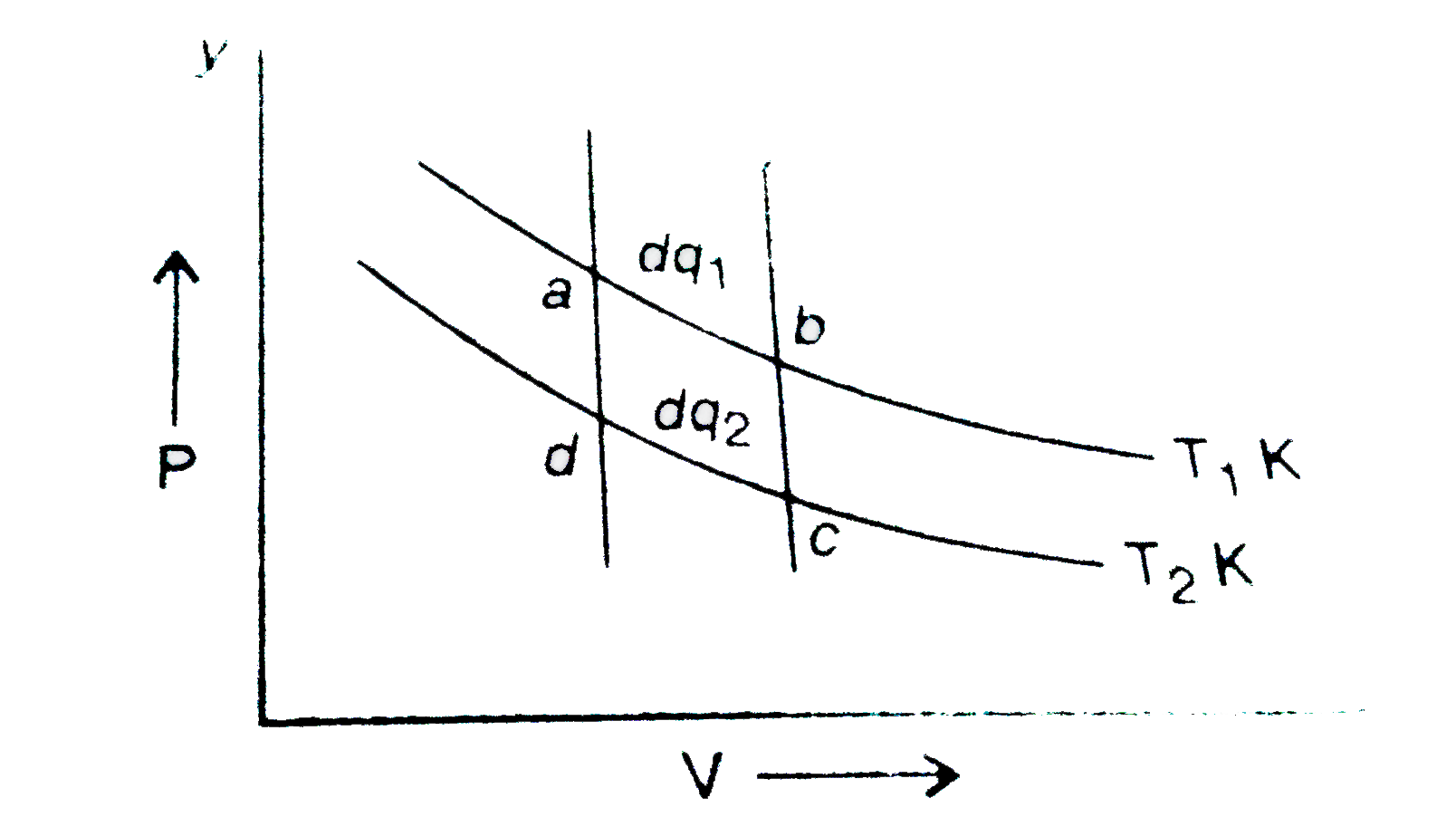
(iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal.

Irrespective of the path of the system in its reversible change, dq/T is same
For entire Carnot cycle
dq1T1−dq2T2=0
∴ΔSuniverse=De<sSsystem+ΔSsurrounding
ΔSSurrounding=q1T1+q2T2 (q term includes their own sign)
bc and da are adiabatics. Let dq1 be the heat supplied to the working system at T1K and dq2 be heat rejected by it to the sink at T2K. All these steps are reversible. In a Carnot cycle.
dq1−dq2dq1=T1−T2T1 or dq1T1=dq2T2
Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc.
Along the path abc, Heat changeTemp.=dq1T1
Along the path adc, Heat changeTemp=dq2T2
In case of spontaneous and irreversible expansion to volume V1+V2, W=0 and so will be ΔU
In the reversible expansion of the gas at TK from volume V1 to V1+V2, heat absorbed ΔU+RTln(V1+V2)V1
(v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V1 which is connected through a stop cock to a completely evacuated vessel B of volume V2. The system is insulated and has temperature TK.

If the stop cock is opened, the gas will attain the volume V1+V2.
In a reversible isothermal expansion of the gas at TK as shown in figure II, the ΔSsystem, ΔSsurroundings and ΔSuniverse will be respectively ?
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
(i) For a reaction entropy change is given by ΔS=∑S(product)−∑S(reactant)
(ii)ΔS=QrevT=WrevT=nRTln(V2/V1)T
=nRTln(V2)V1=nRln(P1)P2
(iii)ΔS=ΔH−TΔS
(iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal.

Irrespective of the path of the system in its reversible change, dq/T is same
For entire Carnot cycle
dq1T1−dq2T2=0
∴ΔSuniverse=De<sSsystem+ΔSsurrounding
ΔSSurrounding=q1T1+q2T2 (q term includes their own sign)
bc and da are adiabatics. Let dq1 be the heat supplied to the working system at T1K and dq2 be heat rejected by it to the sink at T2K. All these steps are reversible. In a Carnot cycle.
dq1−dq2dq1=T1−T2T1 or dq1T1=dq2T2
Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc.
Along the path abc, Heat changeTemp.=dq1T1
Along the path adc, Heat changeTemp=dq2T2
In case of spontaneous and irreversible expansion to volume V1+V2, W=0 and so will be ΔU
In the reversible expansion of the gas at TK from volume V1 to V1+V2, heat absorbed ΔU+RTln(V1+V2)V1
(v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V1 which is connected through a stop cock to a completely evacuated vessel B of volume V2. The system is insulated and has temperature TK.
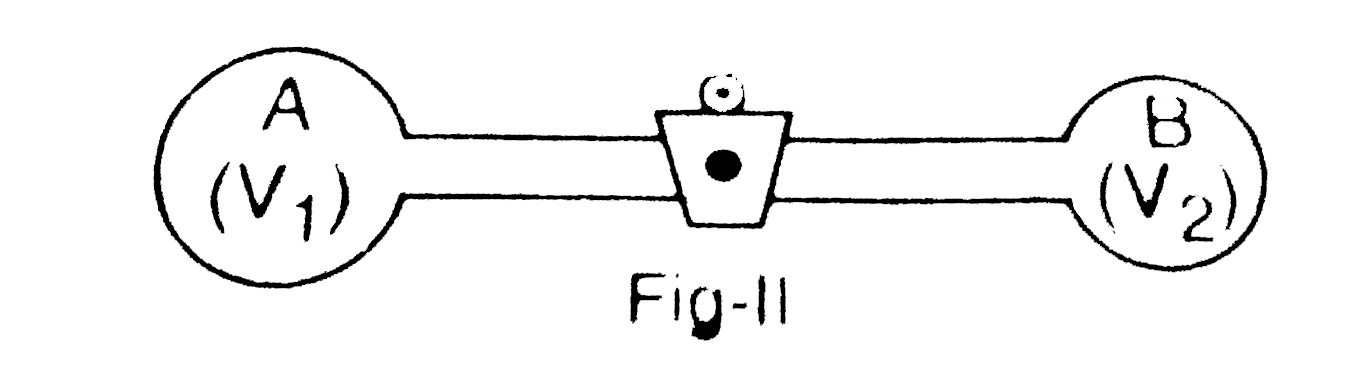
If the stop cock is opened, the gas will attain the volume V1+V2.
In figure I, which is a reversible cyclic process, what will be the value of ΔU, ΔH, ∮dqT respectively ?
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
(i) For a reaction entropy change is given by ΔS=∑S(product)−∑S(reactant)
(ii)ΔS=QrevT=WrevT=nRTln(V2/V1)T
=nRTln(V2)V1=nRln(P1)P2
(iii)ΔS=ΔH−TΔS
(iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal.
Irrespective of the path of the system in its reversible change, dq/T is same
For entire Carnot cycle
dq1T1−dq2T2=0
∴ΔSuniverse=De<sSsystem+ΔSsurrounding
ΔSSurrounding=q1T1+q2T2 (q term includes their own sign)
bc and da are adiabatics. Let dq1 be the heat supplied to the working system at T1K and dq2 be heat rejected by it to the sink at T2K. All these steps are reversible. In a Carnot cycle.
dq1−dq2dq1=T1−T2T1 or dq1T1=dq2T2
Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc.
Along the path abc, Heat changeTemp.=dq1T1
Along the path adc, Heat changeTemp=dq2T2
In case of spontaneous and irreversible expansion to volume V1+V2, W=0 and so will be ΔU
In the reversible expansion of the gas at TK from volume V1 to V1+V2, heat absorbed ΔU+RTln(V1+V2)V1
(v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V1 which is connected through a stop cock to a completely evacuated vessel B of volume V2. The system is insulated and has temperature TK.
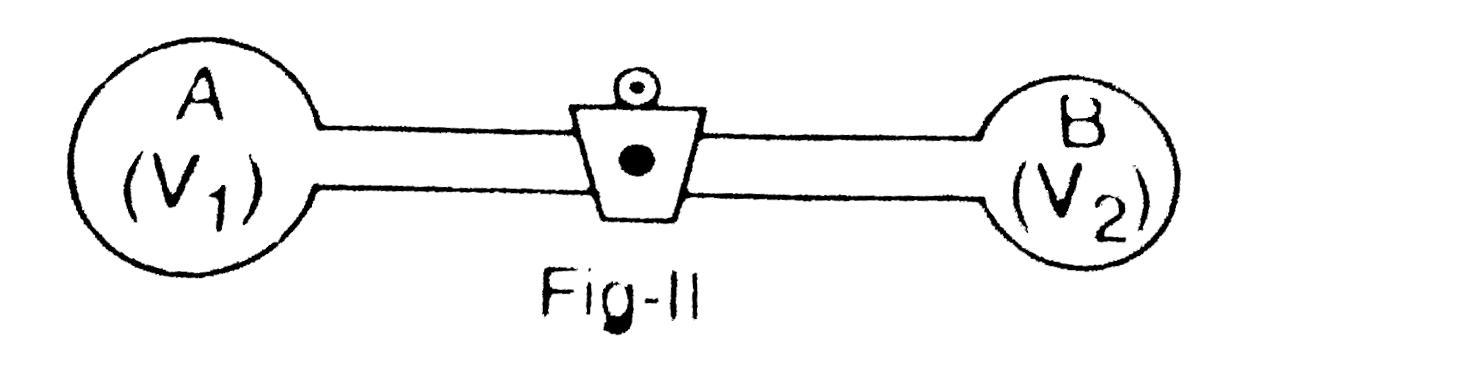
If the stop cock is opened, the gas will attain the volume V1+V2.
In the figure-I, what will be the value of dqT along the line bc ?
View Solution
