Displacement OF Centre OF Mass
Step by step video solution for Displacement OF Centre OF Mass by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Centre Of Mass|OMR
View SolutionA particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)None
View Solution
Knowledge Check
A rod AB of length 1m is placed at the edge for a smooth table as shown in figure. It is hit horizontally at point B. If the displacement of centre of mass m in 1s is 5√2m. The angular velocity of the rod is (g=10m/s2)
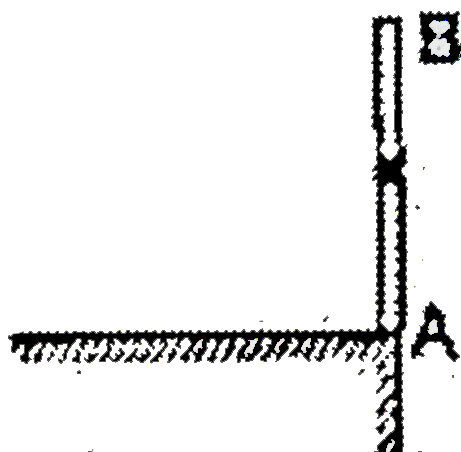 A30rad/sB20rad/sC10rad/sD5rad/s
A30rad/sB20rad/sC10rad/sD5rad/sAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.A√2k3mB3x√k2mCx√3k2mDnone of theseAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

What is the loss in the energy of the system due to breaking of B?A38kx2B34kx2C18kx2D58kx2
Motion OF Centre OF Mass
View SolutionTwo boys A and B of masses 60kg and 40kg respectively are at the ends of a 4m long boat of mass 100kg which is on water in lake and the system is at rest.If the boys meet at the centre of the boat then find the displacement of centre of mass of the boat in meter (neglect friction between water and boat)
View SolutionA light inextensible string, passing over a pulley, supports two particles 1 and 2 at its ends. An insect of mass m is sitting on particle 2 and the system is in equilibrium. The sum of masses of particles and the insect is M. Now the insect crawls a distance x up relative to the string. Find the displacement of centre of mass of the system of two particles and the insect. In which direction does the centre of mass move and why ?
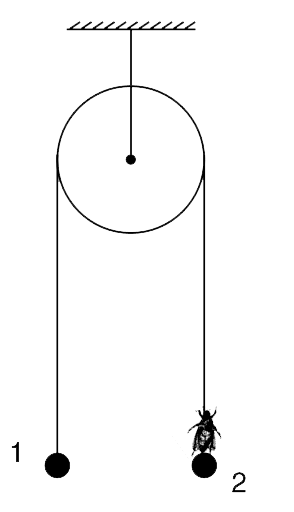
View SolutionProperties OF Centre OF Mass
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
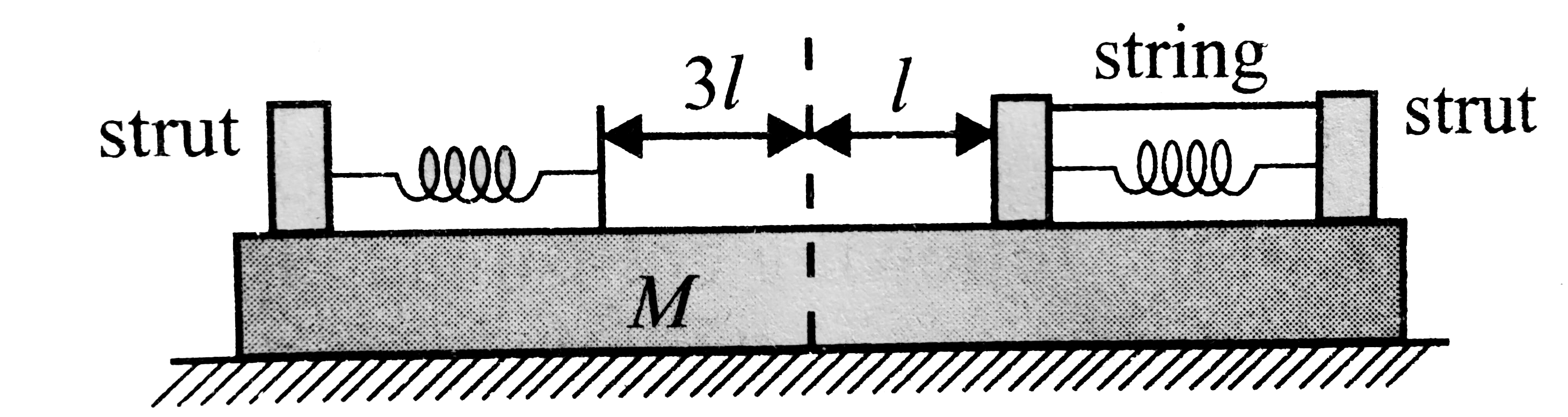
The maximum displacement of the plank is
View Solution
