Discussion OF Exercise-2|| Condition OF Three points be collinear|| Area OF trapezium|| Parallelogram|| Triangle || Plotting Trapezium||Rectangle||Square||Quadrilateral|| Summary
Step by step video solution for Discussion OF Exercise-2|| Condition OF Three points be collinear|| Area OF trapezium|| Parallelogram|| Triangle || Plotting Trapezium||Rectangle||Square||Quadrilateral|| Summary by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Chapter Test Discussion OF -1,2,3,4||Condition OF collinearity OF Three points
View SolutionDiscussion OF example || Mid-point OF two points P and Q || Section formula based questions || Properties OF Parallelogram ||Rectangle || Rhombus || Square
View SolutionDiscussion OF Exemplar Question and Exercise-12.1||Heron's formula||If side OF triangle is lemda square times OF old triangle||Area OF Equilateral ||Isosceles and Right angle triangle
View SolutionNecessary Condition For Equal to be Parallelogram||Parallelogram to be Rectangle||Parallelogram to be rhombus||Rhombus to be square and Rectangle to be square||Ex-8.1 Discussion
View SolutionDiagonals necessarily bisect opposite angles in a
rectangle(b) parallelogram (c)isosceles trapezium (d) square
View SolutionDiscussion OF Ex-12.2 and Examples ||Application OF Heron formula||ProOF OF area OF rhombus=1/2d1d2||Area OF trapezium=1/2(sum OF parallel sides)(distance between parallel sides) || Area OF quadrilateral using Heron's formula
View SolutionArea OF Triangle and Polygon and Condition OF Collinearity OF 3 points
View SolutionWhich of the following is point symmetric? (a) Equilateral triangle (b) Trapezium (c) Rectangle (d) None of these
View SolutionAngle sum Properties OF Quadrilateral || Triangle|| Types OF Quadrilateral|| trapezium|| Rectangle|| Square|| Parallelogram|| Rhombus|| nth side polygon||Interior/Exterior angle properties|| Angle sum properties OF nth side polygon
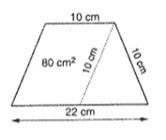
View SolutionIn Figure, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium. (Figure)
View Solution
