Tangential || Normal Acceleration || Radius OF Curvature
Step by step video solution for Tangential || Normal Acceleration || Radius OF Curvature by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A psrticle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2A particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2
Non-uniform circular motion: radial & tangential acceleration| Radius of curvature
View SolutionComponents OF Acceleration in Circular Motion || Radial Acceleration || Tangential Acceleration || Dynamics OF Circular Motion || Examples on Radial & Tangential Acceleration
View SolutionRadial and Tangential Acceleration
View SolutionA particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
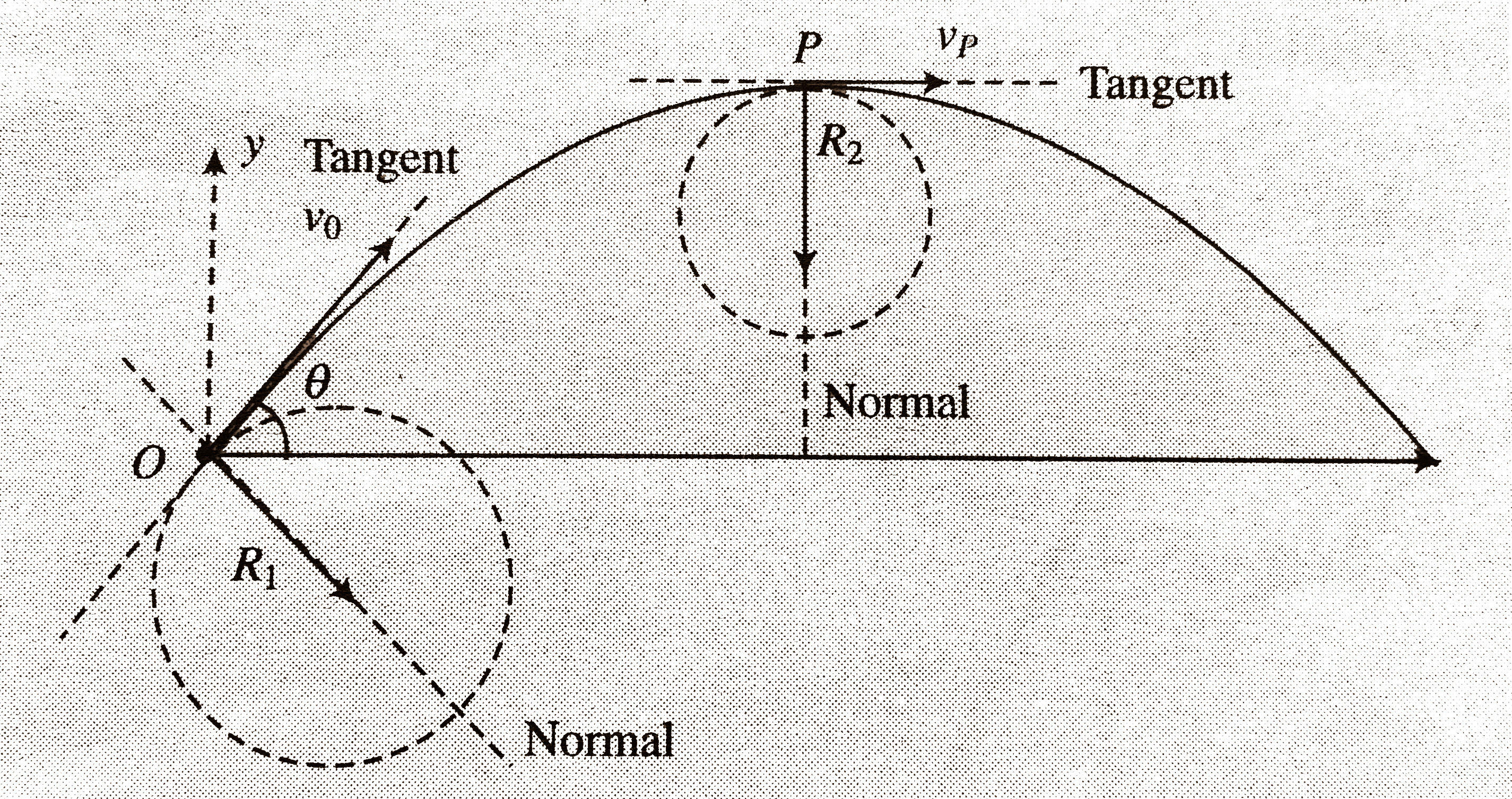 .
.
View SolutionAcceleration in circular motion|| Tangential acceleration|| Radial acceleration|| Shape OF path & net Acceleration
View SolutionThe tangential and radial acceleration of a particle are a(t) and a(r) respectively. The motion of a particle is circular if
View Solution
