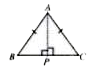
In a ,AB = AC and , then :
AB=AD
The correct Answer is:B
To solve the problem step by step, we will analyze the triangle ABC where AB = AC and AD is perpendicular to BC.
Step 1: Understand the Triangle
We have triangle ABC where:
- AB = AC (This means triangle ABC is isosceles)
- AD is perpendicular to BC (This means that AD forms a right angle with BC)
Step 2: Identify the Points
Let:
- A be the vertex opposite to the base BC.
- B and C be the other two vertices.
- D be the foot of the perpendicular from A to BC.
Step 3: Analyze the Isosceles Triangle
Since AB = AC, the angles opposite these sides will also be equal. Therefore:
- Let angle ABC = angle ACB = x (for some angle x).
- The angle at A (angle BAC) will then be 180° - 2x.
Step 4: Use Right Triangle Properties
In right triangle ABD:
- AD is the height from A to BC.
- By the properties of triangles, we can relate the sides using trigonometric ratios.
Step 5: Compare the Lengths
We need to compare the lengths of AB and AD:
- In any triangle, the length of the side opposite an angle is greater than the length of the altitude from that angle to the opposite side.
- Thus, since AB is opposite angle A, and AD is the altitude, we can conclude that:
AB>AD
Conclusion
From the analysis, we find that the length of side AB is greater than the length of altitude AD.
Final Answer
AB > AD
We have triangle ABC where:
- AB = AC (This means triangle ABC is isosceles)
- AD is perpendicular to BC (This means that AD forms a right angle with BC)
Let:
- A be the vertex opposite to the base BC.
- B and C be the other two vertices.
- D be the foot of the perpendicular from A to BC.
Since AB = AC, the angles opposite these sides will also be equal. Therefore:
- Let angle ABC = angle ACB = x (for some angle x).
- The angle at A (angle BAC) will then be 180° - 2x.
In right triangle ABD:
- AD is the height from A to BC.
- By the properties of triangles, we can relate the sides using trigonometric ratios.
We need to compare the lengths of AB and AD:
- In any triangle, the length of the side opposite an angle is greater than the length of the altitude from that angle to the opposite side.
- Thus, since AB is opposite angle A, and AD is the altitude, we can conclude that:
AB>AD
From the analysis, we find that the length of side AB is greater than the length of altitude AD.
AB > AD
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
AADBBECCFDNone of these - Question 2 - Select One
In a △ABC,AC=BC, Point D lies on BC such that CD=AD=AB. Find ∠ACB.
AA)18∘BB)30∘CC)36∘DD)48∘ - Question 3 - Select One
In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
A√3172cmB√1192cmC√1152cmD√3132cm
In △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn △ABC, ∠ABC=90∘ and BD⊥AC. if AD=4 cm and CD=5 cm, then BD is equal to:
△ABC में, ∠ABC=90∘ और BD⊥AC है| यदि AD=4 cm और CD=5 cm तो BD किसके समान होगा?View SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
 View Solution
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View SolutionIn triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View Solution

