In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
25:49
49:25
6:1
5:7
The correct Answer is:D
To find the ratio BD:CD in triangle ABC where AB=5cm, AC=7cm, and AD is the angle bisector of ∠A, we can use the Angle Bisector Theorem.
1. Understand the Angle Bisector Theorem:
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle. In this case, it can be expressed as:
BDCD=ABAC
2. Substitute the Known Values:
From the problem, we know:
- AB=5cm
- AC=7cm
Now, substituting these values into the ratio:
BDCD=57
3. Conclusion:
Therefore, the ratio BD:CD is:
BD:CD=5:7
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle. In this case, it can be expressed as:
BDCD=ABAC
From the problem, we know:
- AB=5cm
- AC=7cm
BDCD=57
Therefore, the ratio BD:CD is:
BD:CD=5:7
Topper's Solved these Questions
Similar Questions
In △ABC, AB=7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC , where D is a point on BC, then BD is equal to:
View SolutionIn △ABC AB = 7 cm, BC =10cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC, where D is a point on BC, then BD is equal to:
यदि त्रिभुज ABC में, AB = 7 सेमी, BC = 10 सेमी तथा AC =8 सेमी है | यदि AD कोण BAC का समद्विभाजक है, जहाँ D, BC पर स्थित एक बिंदु है, तो BD का मान किसके बराबर है ?
View Solution
Knowledge Check
In ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
A25:49B49:25C6:1D5:7In a triangle ABC. AC = 5 cm, AB = 7 cm, BC=√39 what is the measure of angle A ? is the measure of angle A ?
A45∘B60∘C90∘D30∘In a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is
A18∘B36∘C54∘D72∘
In triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View SolutionIn aΔABC it is given that AB=6cm,AC=8cmandAD is the bisector of ∠A. Then BD:DC=?
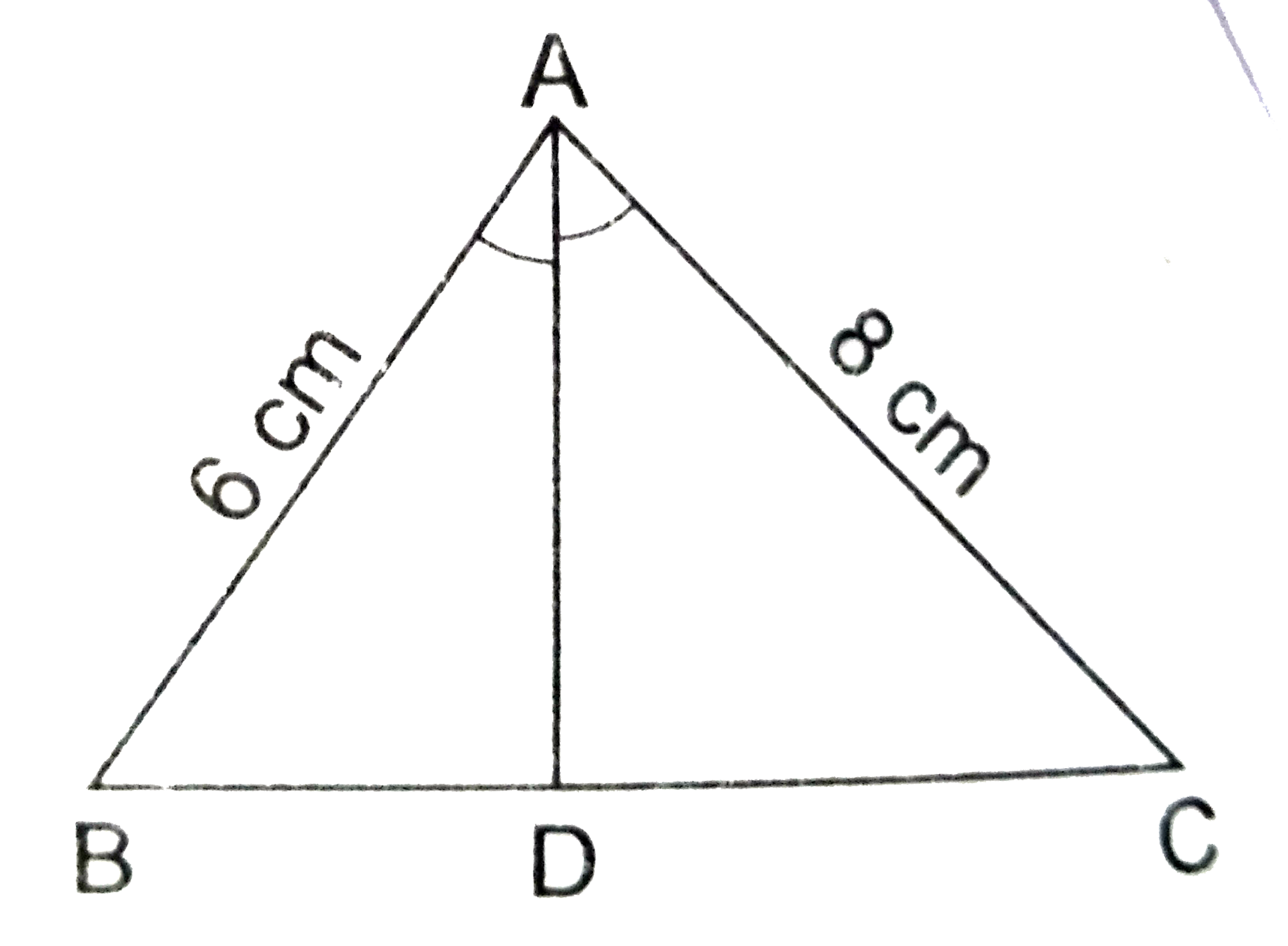
View SolutionIn a ΔABC,∠A=120∘,AB=20cm,AC=30cm find the angle bisector AD .
View SolutionThe ratio of the length and the breadth of a rectangle is 4 : 3 and the area of the rectangle is 1728 sq cm. What is the ratio of the breadth and the area of the rectangle ?
View SolutionIn a △ABC,AD is the angle bisector of ∠CAB and a median to BC. If AC=15 cm, find AB.
View Solution
