In ABC, G is the centroid, AB = 15 cm, BC = 18 cm and AC = 25 cm. Find GD, where D is the mid-point of BC.
13√86 cm
23√86 cm
83√15
none of these
The correct Answer is:B
To find the length GD in triangle ABC where G is the centroid and D is the midpoint of side BC, we can follow these steps:
Step 1: Understand the triangle and its properties
- We have triangle ABC with sides AB = 15 cm, BC = 18 cm, and AC = 25 cm.
- D is the midpoint of BC, so BD = DC = 9 cm.
Hint: Remember that the centroid divides each median in a 2:1 ratio.
Step 2: Calculate the lengths of the segments
- Since D is the midpoint of BC, we have:
- BD = DC = 9 cm.
Step 3: Find the length of the median AD
- To find GD, we first need to calculate the length of the median AD using the formula for the length of a median:
ma=√2b2+2c2−a24
where a=BC, b=AC, and c=AB.
Here, a=18 cm, b=25 cm, and c=15 cm.
Step 4: Substitute the values into the median formula
- Substitute the values into the median formula:
ma=√2(252)+2(152)−(182)4
Calculating each term:
- 252=625
- 152=225
- 182=324
Now substituting these values:
ma=√2(625)+2(225)−3244=√1250+450−3244=√13764=√344
Step 5: Calculate GD
- The centroid G divides the median AD in the ratio 2:1. Therefore, the length GD is:
GD=13×ma=13×√344
Calculating √344:
- √344≈18.52 (approximately).
Thus,
GD≈18.523≈6.17 cm
Final Answer
GD is approximately 6.17 cm.
---
- We have triangle ABC with sides AB = 15 cm, BC = 18 cm, and AC = 25 cm.
- D is the midpoint of BC, so BD = DC = 9 cm.
- Since D is the midpoint of BC, we have:
- BD = DC = 9 cm.
- To find GD, we first need to calculate the length of the median AD using the formula for the length of a median:
ma=√2b2+2c2−a24
Here, a=18 cm, b=25 cm, and c=15 cm.
- Substitute the values into the median formula:
- 252=625
- 152=225
- 182=324
- The centroid G divides the median AD in the ratio 2:1. Therefore, the length GD is:
- √344≈18.52 (approximately).
GD is approximately 6.17 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC,AB=8 cm, BC=15 cm and AC=17 cm. find the largest angle.
A∠AB∠CC∠BDNone of these - Question 2 - Select One
△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336625D625336 - Question 3 - Select One
△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336/625D625/336
In a triangle ABC, if AB = 20 cm, AC = 21 cm and BC = 29 cm, then find the distance vertex A and mid point of BC.
View SolutionIn ΔABC, AB = 15 cm, BC = 12 cm and AC = 17 cm . Find out the greatest and smallest angle of ΔABC .
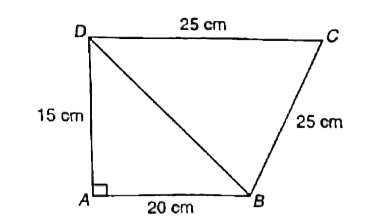
View SolutionIn the given figure AD=15cm,AB=20cmandBC=CD=25cm. Find the area of □ABCD:
 View Solution
View Solution□ABCD is a parallelogram, AB=14cm,BC=18cmandAC=16cm. Find the length of the other diagonal:
View Solution□ABCD is a parallelogram, AB=14cm,BC=18cmandAC=16cm. Find the length of the other diagonal:
View Solution

