AB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :

rectangle
square
parallelogram
none of these
The correct Answer is:A
Step by step video & image solution for AB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
AB and CD are two parallel lines and a transversal 'l' intersects these lines at X and Y respectively Prove that the bisectors of interior angles from a parallelogram whose each angle is 90∘.
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
Knowledge Check
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ ,then ∠CFQ will be :
A70∘B55∘C110∘D125∘AB and CD are two parallel lines, PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ then ∠CFQ will be :
A70∘B55∘C110∘D125∘Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
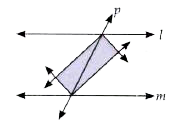 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
View SolutionTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View Solution
