ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AN=√3AB
AN=2AB
AN2=32AB2
AN2=2AB2
The correct Answer is:B
Step by step video, text & image solution for ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
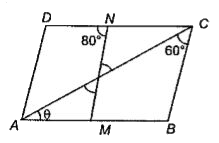 A20∘B30∘C40∘D10∘
A20∘B30∘C40∘D10∘ - Question 2 - Select One
In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
 A20*B30*C40*D10*
A20*B30*C40*D10* - Question 3 - Select One
ABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
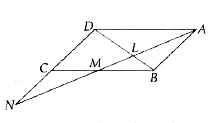
Given that DL =3LB , find ABCN .A3/2B1/2C4/5D1/4
In the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
View Solution