Question

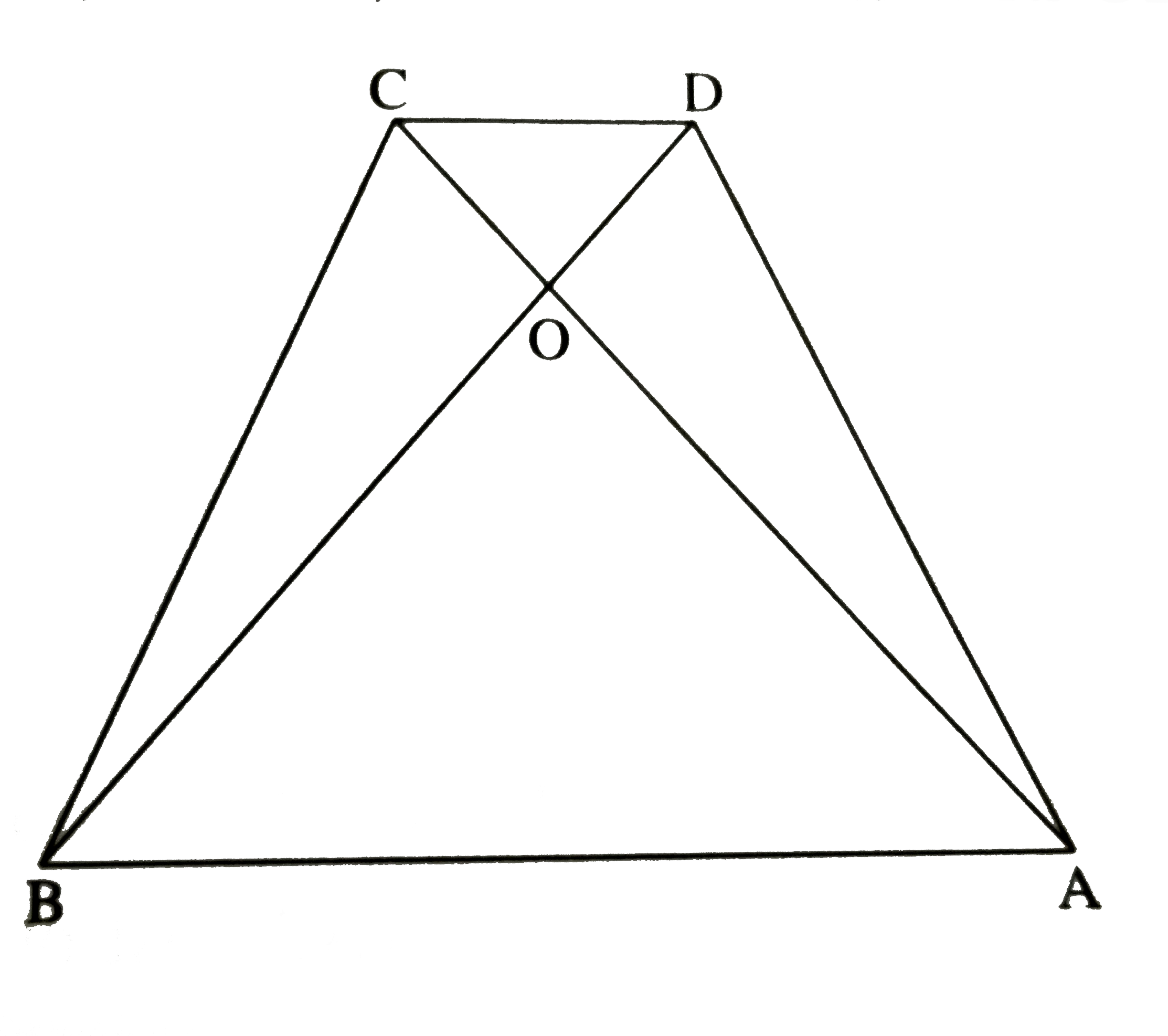
In a trapezium ABCD, where AB||CD and diagonal AC intersects the other diagonal BD at O. Which of the followings are always correct ?
$\left(i\right)\frac{DO}{AO}=\frac{CO}{BO}$ $\left(ii\right)\frac{DO}{OC}=\frac{AO}{OB}$
$\left(iii\right)\frac{DO}{OB}=\frac{CO}{OA}$

Options

A. A)only (i) and (ii)
B. B)only (ii) and (iii)
C. C)only (i) and (iii)
D. D)only (iii)

Answer

D

Explanation

To solve the problem, we need to analyze the trapezium ABCD where AB is parallel to CD, and the diagonals AC and BD intersect at point O. We will evaluate the three statements provided to determine which one(s) are always correct.

Step 1: Understanding the trapezium and the properties of similar triangles
- Since AB is parallel to CD, we can use the properties of similar triangles formed by the diagonals.
- When two lines are crossed by a pair of parallel lines, the alternate interior angles are equal.

Step 2: Identify the angles
- Let’s denote the angles formed at point O:
- ∠AOB = α
- ∠COD = α (alternate interior angles)
- ∠AOD = β
- ∠BOC = β (alternate interior angles)
- ∠AOC = θ
- ∠BOD = θ (alternate interior angles)

Step 3: Analyze the triangles
- From the angles identified, we can see that:
- Triangle AOB is similar to triangle COD (by AA similarity criterion).
- Triangle AOD is similar to triangle BOC (by AA similarity criterion).

Step 4: Set up the ratios from the similar triangles
1. From triangles AOB and COD:
\( \frac{DO}{AO} = \frac{CO}{BO} \)
This corresponds to Statement (i).

2. From triangles AOD and BOC:
\( \frac{DO}{OC} = \frac{AO}{OB} \)
This corresponds to Statement (ii).

3. From triangles AOB and BOC:
\( \frac{DO}{OB} = \frac{CO}{OA} \)
This corresponds to Statement (iii).

Step 5: Evaluate the statements
- Statement (i): \((DO)/(AO) = (CO)/(BO)\) is correct.
- Statement (ii): \((DO)/(OC) = (AO)/(OB)\) is correct.
- Statement (iii): \((DO)/(OB) = (CO)/(OA)\) is correct.

Conclusion
All three statements are correct based on the properties of similar triangles in trapezium ABCD.

Final Answer
All statements (i), (ii), and (iii) are correct.

---