If P is a point within a rectangle ABCD, then:
AP2+PC2=BP2+PD2
AP2+BP2=PC2+PD2
AP+PC=BP+PD
AP×PC=BP×PD
The correct Answer is:A
To solve the problem, we need to establish the relationship between the distances from point P to the vertices of rectangle ABCD. Let's denote the distances as follows:
- AP = a
- BP = b
- CP = c
- DP = d
We will analyze the options given in the question.
1. Understanding the Geometry:
- We have a rectangle ABCD with vertices A, B, C, and D.
- Point P is located inside the rectangle.
2. Using the Distance Formula:
- The distances from point P to the vertices can be represented as:
- AP = distance from P to A
- BP = distance from P to B
- CP = distance from P to C
- DP = distance from P to D
3. Analyzing the Options:
- Option 1: AP2+PC2=BP2+PD2
- Option 2: AP2+BP2=PC2+PD2
- Option 3: AP+PC=BP+PD
- Option 4: AP⋅PC=BP⋅PD
4. Verifying Option 1:
- According to the properties of rectangles, we can use the Pythagorean theorem to establish relationships between these distances.
- By applying the theorem, we can derive that:
AP2+PC2=BP2+PD2
- This holds true as we can visualize that the sum of the squares of the distances from point P to opposite corners of the rectangle are equal.
5. Conclusion:
- Therefore, the correct relationship is given by Option 1:
AP2+PC2=BP2+PD2
- BP = b
- CP = c
- DP = d
- We have a rectangle ABCD with vertices A, B, C, and D.
- Point P is located inside the rectangle.
- The distances from point P to the vertices can be represented as:
- AP = distance from P to A
- BP = distance from P to B
- CP = distance from P to C
- DP = distance from P to D
- Option 1: AP2+PC2=BP2+PD2
- Option 2: AP2+BP2=PC2+PD2
- Option 3: AP+PC=BP+PD
- Option 4: AP⋅PC=BP⋅PD
- According to the properties of rectangles, we can use the Pythagorean theorem to establish relationships between these distances.
- By applying the theorem, we can derive that:
AP2+PC2=BP2+PD2
- This holds true as we can visualize that the sum of the squares of the distances from point P to opposite corners of the rectangle are equal.
- Therefore, the correct relationship is given by Option 1:
AP2+PC2=BP2+PD2
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a rectangle with A(−1,2),B(3,7) and AB:BC=4:3. If P is the centre of the rectangle, then the distance of P from each corner is equal to
A√142B3√414C2√413D5√418Let X be any point within a square ABCD. On AX, a square, AXYZ is described such that D is within it. Which one of the following is correct ?
Aa. AX = DZBb. ∠ADZ∠BAXCc. AD=DZDd. BX=DZ
If O is a point within a quadrilateral ABCD, show that OA+OB+OC+OD>AC+BD.
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
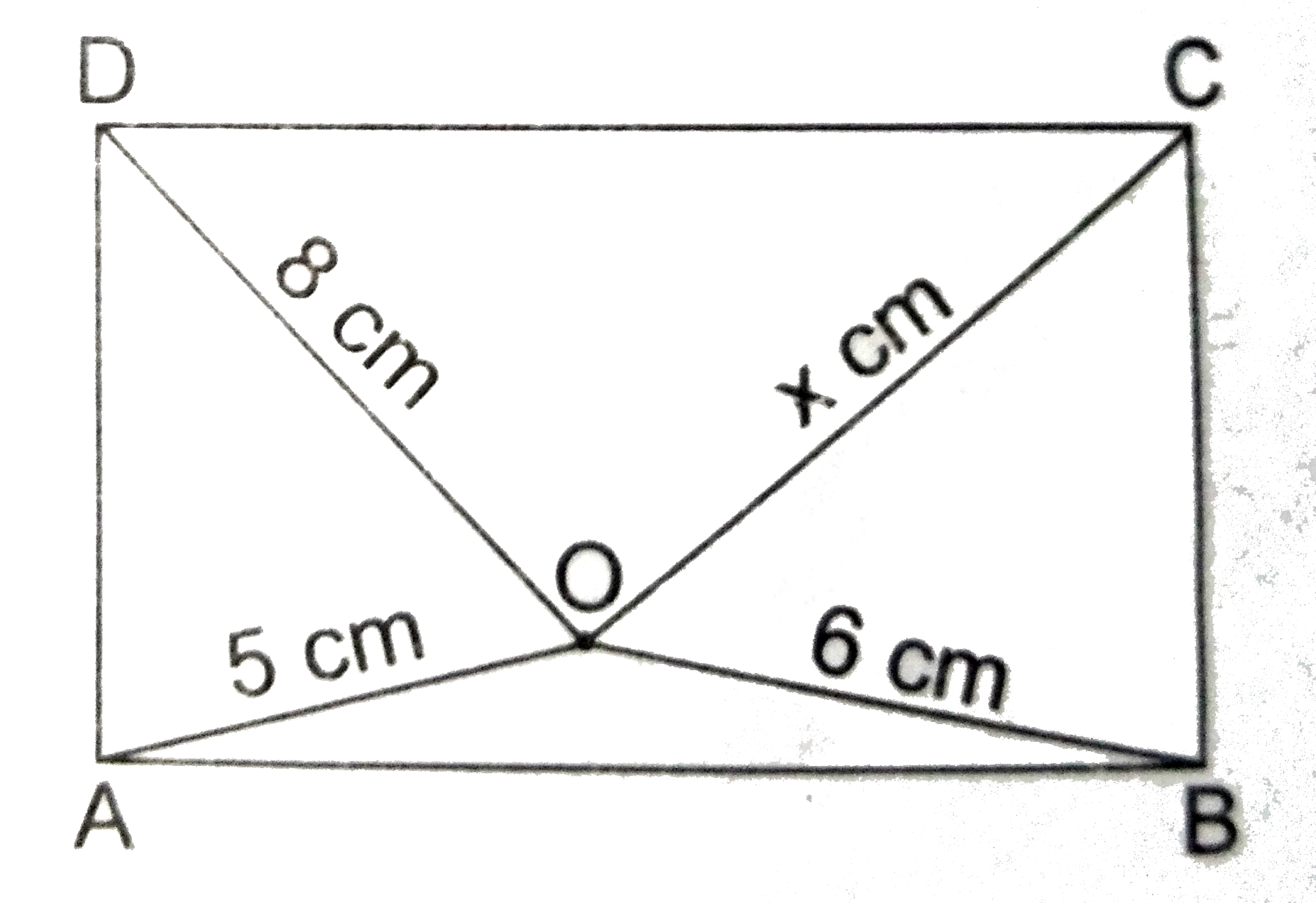
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionQ is a point interior of a rectangle ABCD . If QA=3cm,QB=4cm and QC=5cm,then length of QD is
View SolutionWhat is the area of rectangle ABCD?

View SolutionABCD is a rectangle. A circle passing through vertex C touches the sides AB and AD at M and N respectively. If the distance lof the line MN from the vertex C is P units then the area of rectangle ABCD is
View Solution
