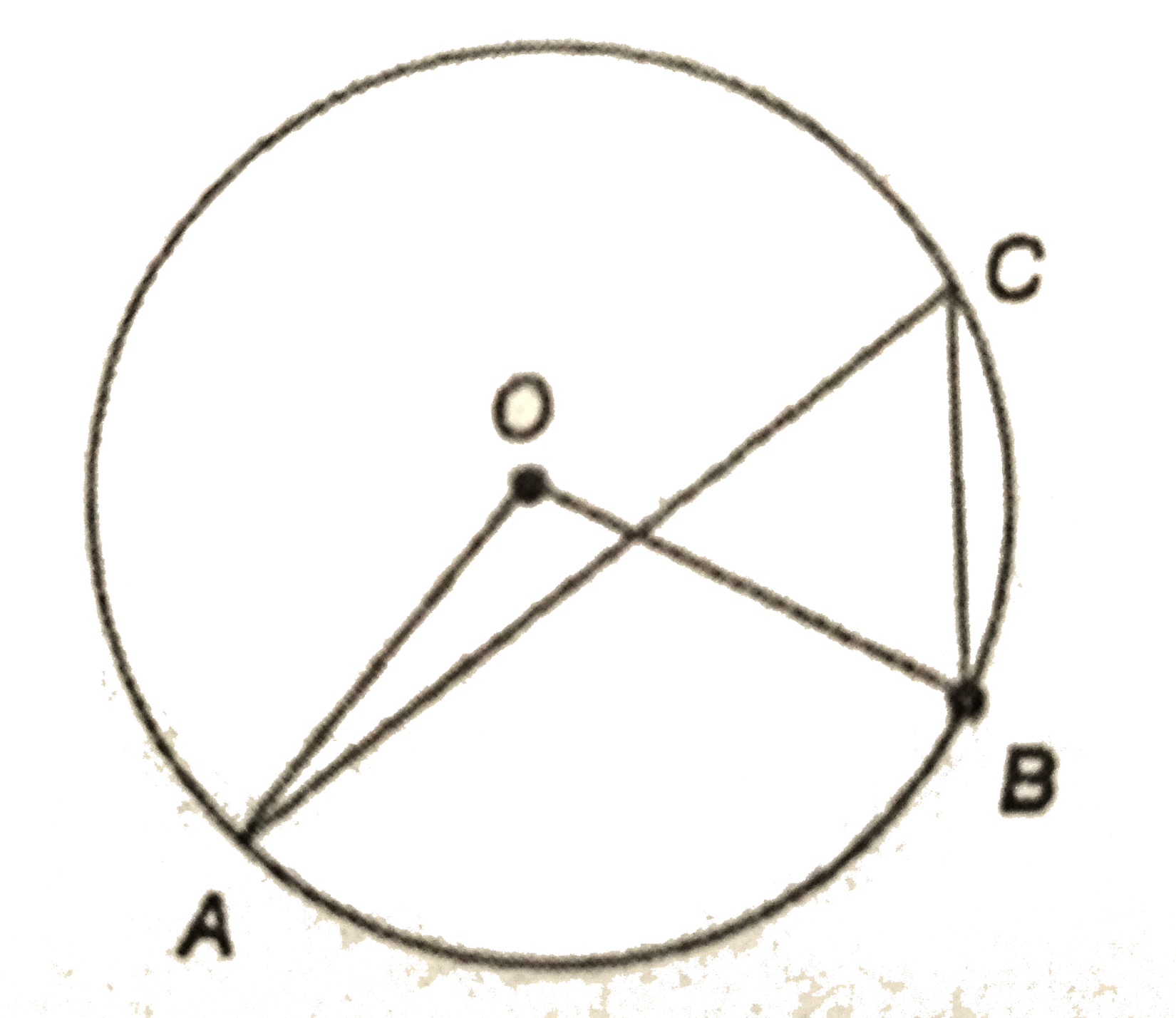Points A,B,C and D are concyclic. BC is the diameter and O is the centre of the circle, ∠BAO=69∘ find ∠DAO+∠DCO
A)138
B)111
C)121
D)none of these
The correct Answer is:B
To solve the problem, we need to find the sum of angles ∠DAO+∠DCO given that points A, B, C, and D are concyclic, with BC as the diameter and O as the center of the circle. We know that ∠BAO=69∘.
1. Identify the Circle and Points:
- Draw a circle with points A, B, C, and D on its circumference.
- Mark BC as the diameter of the circle, and O as the center of the circle.
2. Label the Angles:
- We know that ∠BAO=69∘.
3. Determine ∠ABO:
- Since OA and OB are radii of the circle, triangle AOB is isosceles.
- Therefore, ∠ABO=∠OAB=69∘.
4. Calculate ∠AOB:
- The sum of angles in triangle AOB is 180∘.
- Thus, ∠AOB=180∘−∠BAO−∠ABO=180∘−69∘−69∘=42∘.
5. Find ∠DAB:
- Since A, B, C, D are concyclic and BC is the diameter, ∠BAC=90∘ (angle subtended by diameter).
- Therefore, ∠DAB+∠BAC=180∘ (opposite angles in cyclic quadrilateral).
- Hence, ∠DAB=180∘−90∘=90∘.
6. Calculate ∠DCO:
- Since ∠DAB=90∘ and ∠BAO=69∘, we can find ∠DAB using the cyclic property.
- ∠DCO=∠DAB−∠BAO=90∘−69∘=21∘.
7. Find ∠DAO+∠DCO:
- We know ∠DAO=∠DAB=90∘.
- Therefore, ∠DAO+∠DCO=90∘+21∘=111∘.
Final Answer:
Thus, ∠DAO+∠DCO=111∘.
---
- Draw a circle with points A, B, C, and D on its circumference.
- Mark BC as the diameter of the circle, and O as the center of the circle.
- We know that ∠BAO=69∘.
- Since OA and OB are radii of the circle, triangle AOB is isosceles.
- Therefore, ∠ABO=∠OAB=69∘.
- The sum of angles in triangle AOB is 180∘.
- Thus, ∠AOB=180∘−∠BAO−∠ABO=180∘−69∘−69∘=42∘.
- Since A, B, C, D are concyclic and BC is the diameter, ∠BAC=90∘ (angle subtended by diameter).
- Therefore, ∠DAB+∠BAC=180∘ (opposite angles in cyclic quadrilateral).
- Hence, ∠DAB=180∘−90∘=90∘.
- Since ∠DAB=90∘ and ∠BAO=69∘, we can find ∠DAB using the cyclic property.
- ∠DCO=∠DAB−∠BAO=90∘−69∘=21∘.
- We know ∠DAO=∠DAB=90∘.
- Therefore, ∠DAO+∠DCO=90∘+21∘=111∘.
Thus, ∠DAO+∠DCO=111∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘ , then ∠AOC is equal to:
 A60∘B80∘C40∘D160∘
A60∘B80∘C40∘D160∘In figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
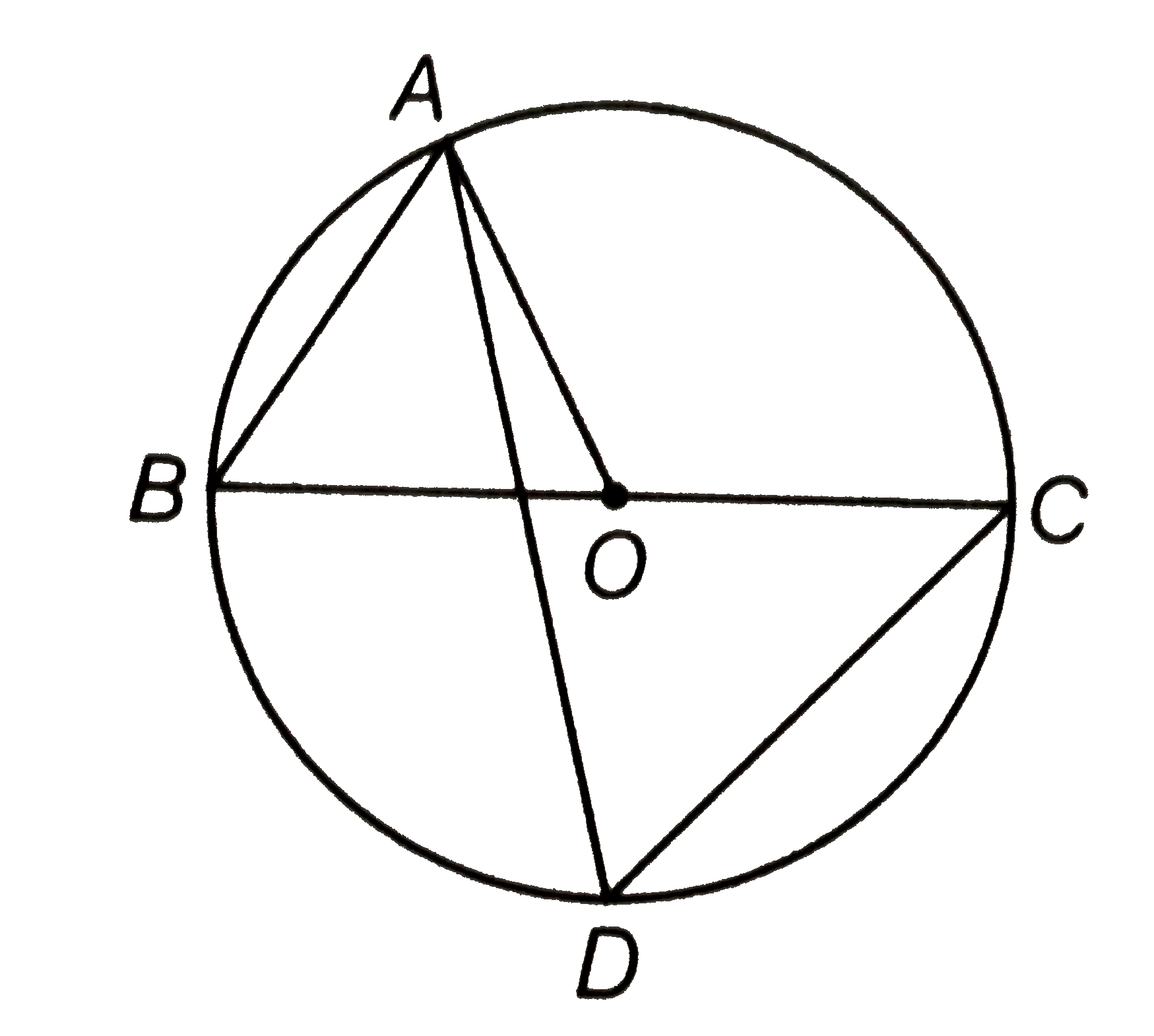 A60∘B45∘C50∘D120∘
A60∘B45∘C50∘D120∘In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘
Two tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionIn the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. ∠BDQ=48∘. Find the ratio of angleDBA:angleDCB.
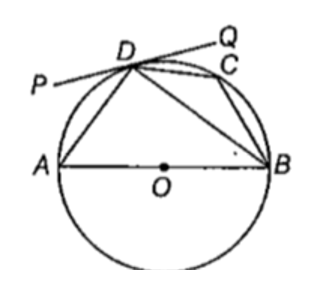
View SolutionIn the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. ∠BDQ=48∘. Find the ratio of angleDBA:angleDCB.

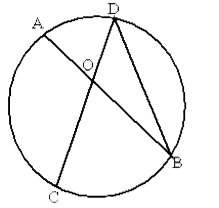
View SolutionAB is a diameter of the circle. Two points C and D are such point that CD = BD. AB and CD intersect at O. If angle ∠AOD=45∘. Find ∠ADC
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
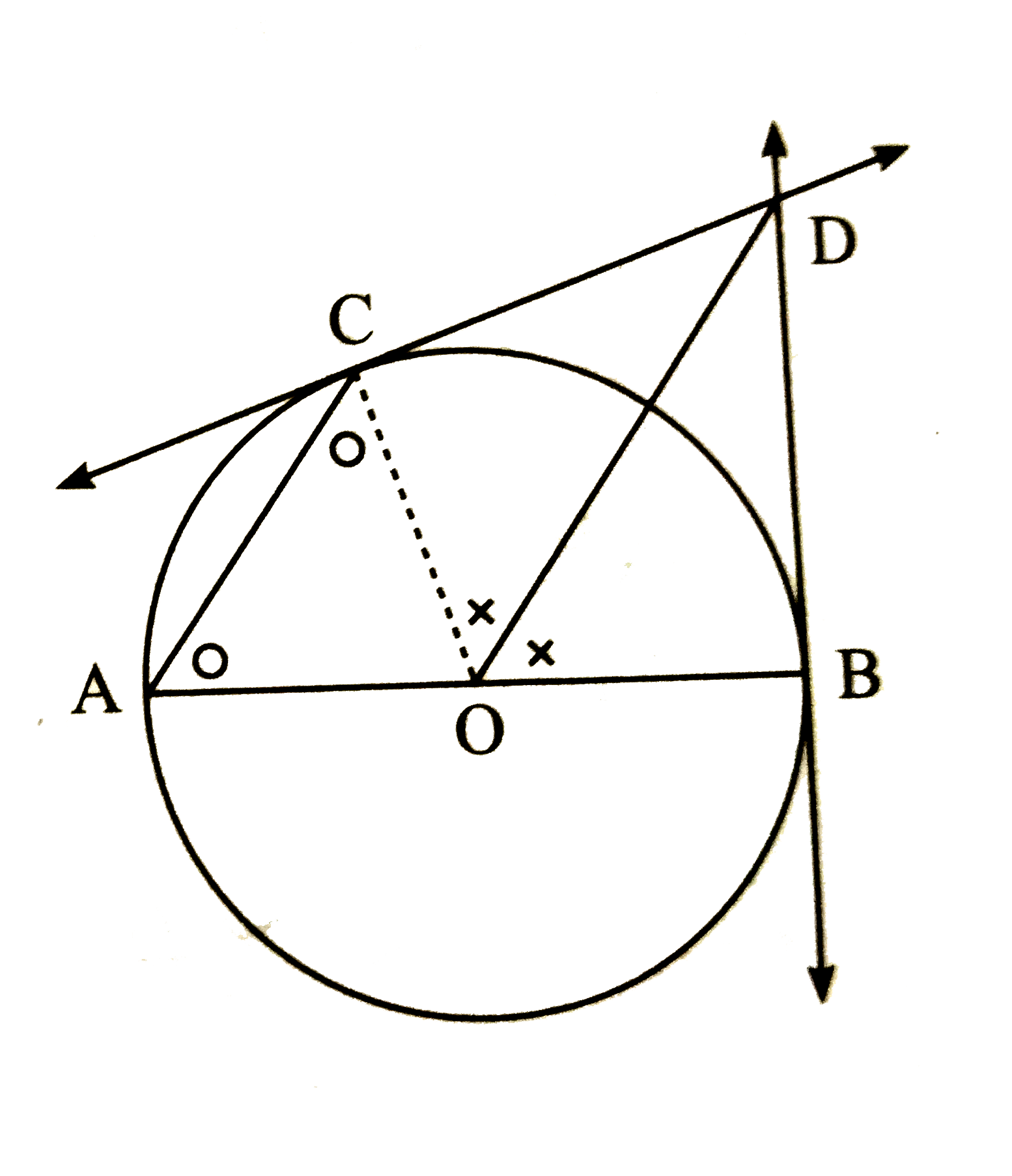
View Solution