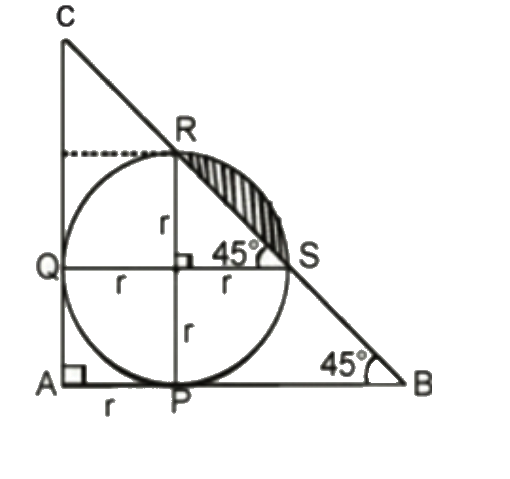
An isoceles right triangl ABC has an incircle with centre O, which touches the sides AB, BC, and AC . Find radius of circle
√2−1 cm
√2−12 cm
1−1√2 cm
none of these
The correct Answer is:A
To find the radius of the incircle of an isosceles right triangle ABC, we can follow these steps:
Step 1: Understand the Triangle
Since triangle ABC is an isosceles right triangle, we can denote the lengths of the two equal sides (legs) as a. The hypotenuse will then be a√2.
Step 2: Calculate the Area of the Triangle
The area A of a right triangle can be calculated using the formula:
A=12×base×height
For triangle ABC, both the base and height are equal to a:
A=12×a×a=a22
Step 3: Calculate the Semi-Perimeter
The semi-perimeter s of triangle ABC is given by:
s=side1+side2+hypotenuse2=a+a+a√22=2a+a√22=a(1+√22)
Step 4: Use the Formula for the Radius of the Incircle
The radius r of the incircle can be calculated using the formula:
r=As
Substituting the values we found:
r=a22a(1+√22)
Step 5: Simplify the Expression
Now we simplify the expression for r:
r=a22a(1+√22)=a2(1+√22)
To simplify further, multiply the numerator and denominator by 2:
r=2a4+2√2=2a(2−√2)(4+2√2)(2−√2)
Using the difference of squares in the denominator:
(4+2√2)(2−√2)=8−4√2+4−2=12−6√2
Thus, the radius simplifies to:
r=2a(2−√2)12−6√2
Step 6: Final Result
Assuming a=1 (for simplicity), we can substitute a into the formula:
r=2(2−√2)12−6√2
Conclusion
The radius of the incircle of the isosceles right triangle ABC is given by the simplified expression above.
---
Since triangle ABC is an isosceles right triangle, we can denote the lengths of the two equal sides (legs) as a. The hypotenuse will then be a√2.
The area A of a right triangle can be calculated using the formula:
A=12×base×height
For triangle ABC, both the base and height are equal to a:
A=12×a×a=a22
The semi-perimeter s of triangle ABC is given by:
s=side1+side2+hypotenuse2=a+a+a√22=2a+a√22=a(1+√22)
The radius r of the incircle can be calculated using the formula:
r=As
Substituting the values we found:
r=a22a(1+√22)
Now we simplify the expression for r:
r=a22a(1+√22)=a2(1+√22)
To simplify further, multiply the numerator and denominator by 2:
r=2a4+2√2=2a(2−√2)(4+2√2)(2−√2)
Using the difference of squares in the denominator:
(4+2√2)(2−√2)=8−4√2+4−2=12−6√2
Thus, the radius simplifies to:
r=2a(2−√2)12−6√2
Assuming a=1 (for simplicity), we can substitute a into the formula:
r=2(2−√2)12−6√2
The radius of the incircle of the isosceles right triangle ABC is given by the simplified expression above.
Topper's Solved these Questions
Similar Questions
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

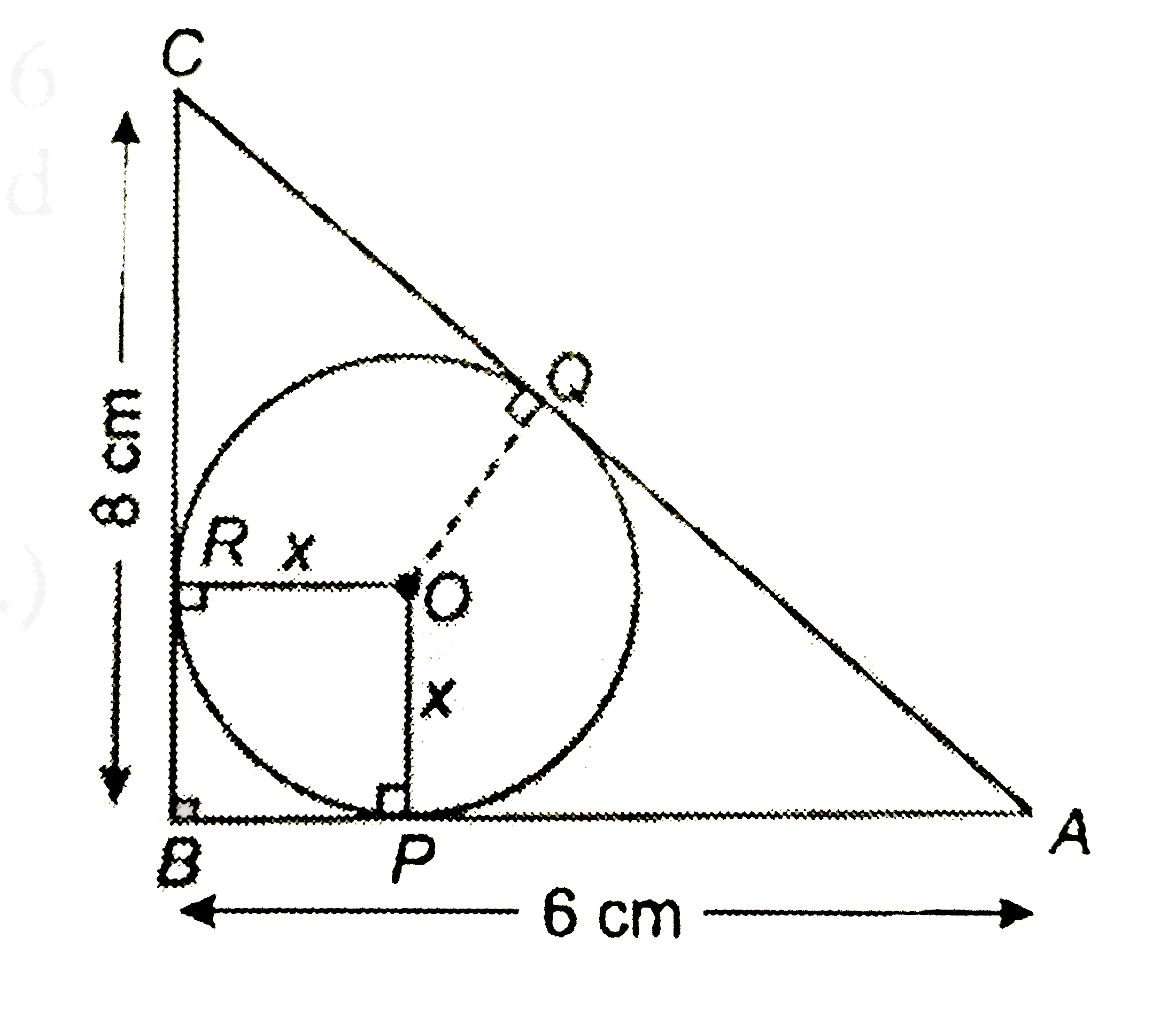
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View Solution
Knowledge Check
An isoceles right triangl ABC has an incircle with centre O, which touches the sides AB, BC, and AC . Find radius of circle
A√2−1 cmB√2−12 cmC1−1√2 cmDnone of theseABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cm
ABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionABC is right angle triangle , (right angled at B ) incircle touches the sides AB, BC & AC at F, E, & D respectively . If BD is prependicular to AC then , find the ratio of AF to FB .
View SolutionThe incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right angled triangle whose radius of circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. The value of r is
View SolutionABC is a triangle. Circles with radii as shown are drawn inside the triangle each touching two sides and the incircle. Find the radius of the incircle of the ΔABC.
View Solution
