Answer the following questions based on the information given below.
In a kite, the shorter diagonal intersects the longer diagonal in the ratio of 6:7. and the longer diagonal of the kite is 52 cm and perimeter of the kite is 208 cm.
If there are four non-overlapping circles inscribed in each of the four triangles formed due to the intersection of two perpendicular diagonals of the kite, find the perimeter of the quadrilateral that is formed by joining the centers of these four circles.
76 cm
2(19+√362)cm
2(19+√360)cm
4√362cm
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
Answer the following questions based on the information given below.
In a kite, the shorter diagonal intersects the longer diagonal in the ratio of 6:7. and the longer diagonal of the kite is 52 cm and perimeter of the kite is 208 cm.
Find the area of the circle inscribed in this kite.A2080 sq. cmB1263 sq. cmC1591 sq. cmD2340 sq. cmIf the side of a rhombus is 20 meters and its shorter diagonal is three - fourths of its longer diagonal, then the area of the rhombus must be
A375 m2B380 m2C384 m2D395 m2In the given kite, y equals
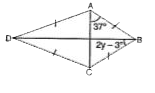 A37∘B28∘C20∘D40∘
A37∘B28∘C20∘D40∘
In the following figure of regular dodecagon find the area of all the four kites, where each of the four kites has two unequal diagonals and the side of each square, each triangle and each kite is 1 cm.

View SolutionA longer side of a parallelogram is 10 cm and the shorter is 6 cm. If the longer diagonal makes an angle 30∘ with the longer side, then the length of the longer diagonal (in cm) is
View SolutionThe perimeter of a rhombus is 52 metres while its longer diagonal is 24 metres .Its Other diagonal is -----
View SolutionThe area of a rhombus is 144 cm and one of its diagonals is double the other. The length of the longer diagonal is
View SolutionThe length of one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of the length of the other diagonal? 45 (b) 25 (c) 34 (d) 14
View Solution
