In a △ABC, AP is the median that intersects QR at O, where Q and R lie on the AB and AC respectively. 2AQ = 3BQ and 3ARn = 4CR, Find the ratio of area of △QOP to that of △ROP.
21:20
9:8
2:1
16:15
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC,DE∣∣BC where D and E are respectively lie on AB and AC and DE:BC=3:5. What is the ratio of area of triangle ABC to area of triangle DAE ?
A3:1B5:3C9:2D25:9The line x + y = p meets the axis of x and y at A and B respectively. A triangle APQ is inscribed in the triangle OAB, O being the origin, with right angle at Q, P and Q lie respectively on OB and AB. If the area of the triangle APQ is 3/8th of the area of the triangle OAB, then AQBQ is equal to
A2B2/3C1/3D3In a△ABC, CP and BQ intersect each other at R inside the triangle, where P and Q lie on the sides AB and AC respectively. ∠BAC=50∘,∠ABC=70∘,∠ACB=∠APQ and PC=BC. Find ∠PBQ.
A10∘B15∘C20∘Dnone of these
In △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn a triangle ABC with ∠BCA=90∘, the perpendicular bisector of AB intersects segments AB and AC at X and Y, respectively. If the ratio of the area of quadrilateral BXYC be the area of triangle ABC is 13:18 and BC=12 then which is the length of AC?
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.

View SolutionIn an isosceles triangle ABC, side BC is distinct from rest of the sides. CD and BE are the medians on AB and AC, respectively. If W,X,Y and Z represents distinct areas in the triangle, find the ratio of W:X:Y:Z
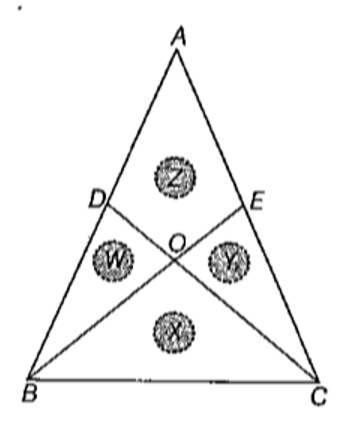
View SolutionIn a triangle ABC point D and E lie on the sides AB and AC, respectively. Lines segments DC and BE intersect inside the triangle at O. The area of △BOC=8sq.cm,△BDO=7sq.cm and △CEO=4sq.cm. Find the area of quadrilateral ADOE.
View Solution
