A point O lies inside a square ABCD such that OB=7 and OD=6, OC=2 find the value of OA?
9
6
5
12
The correct Answer is:A
To find the value of OA given the distances OB, OD, and OC, we can use the property of a square concerning the distances from a point inside the square to its vertices. Here’s a step-by-step solution:
Step 1: Understand the Geometry
We have a square ABCD with a point O inside it. The distances from point O to the vertices are given:
- OB = 7
- OD = 6
- OC = 2
We need to find the distance OA.
Step 2: Use the Property of the Square
There is a property that states for any point O inside a square ABCD:
OA2+OC2=OB2+OD2
Step 3: Substitute the Known Values
We can substitute the known distances into the equation:
- OA^2 + OC^2 = OB^2 + OD^2
- OA^2 + 2^2 = 7^2 + 6^2
Step 4: Calculate the Squares
Now, we calculate the squares of the distances:
- OC^2 = 2^2 = 4
- OB^2 = 7^2 = 49
- OD^2 = 6^2 = 36
Step 5: Set Up the Equation
Substituting these values into the equation gives:
OA2+4=49+36
Step 6: Simplify the Right Side
Now, simplify the right side:
OA2+4=49+36=85
Step 7: Solve for OA^2
Now, isolate OA^2:
OA2=85−4
OA2=81
Step 8: Take the Square Root
Finally, take the square root to find OA:
OA=√81=9
Conclusion
Thus, the value of OA is 9.
---
We have a square ABCD with a point O inside it. The distances from point O to the vertices are given:
- OB = 7
- OD = 6
- OC = 2
There is a property that states for any point O inside a square ABCD:
OA2+OC2=OB2+OD2
We can substitute the known distances into the equation:
- OA^2 + OC^2 = OB^2 + OD^2
- OA^2 + 2^2 = 7^2 + 6^2
Now, we calculate the squares of the distances:
- OC^2 = 2^2 = 4
- OB^2 = 7^2 = 49
- OD^2 = 6^2 = 36
Substituting these values into the equation gives:
OA2+4=49+36
Now, simplify the right side:
OA2+4=49+36=85
Now, isolate OA^2:
OA2=85−4
OA2=81
Finally, take the square root to find OA:
OA=√81=9
Thus, the value of OA is 9.
Topper's Solved these Questions
Similar Questions
O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
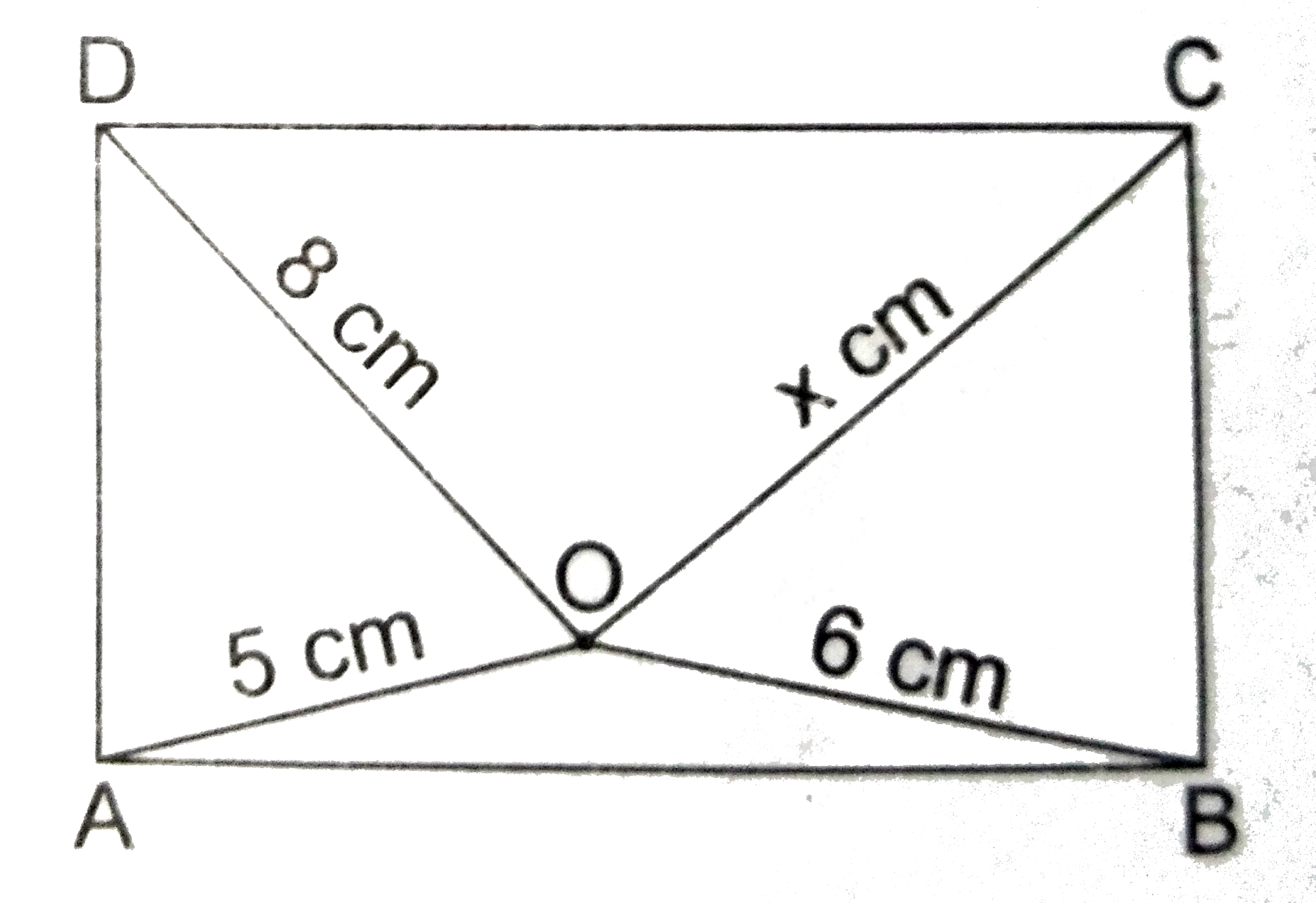
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
 View Solution
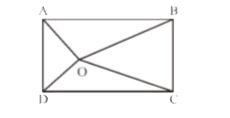
View SolutionO is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
AA)3√3BB)6.67CC)3√2DD)4√2 - Question 2 - Select One
A point O lies inside a square ABCD such that OB=7 and OD=6, OC=2 find the value of OA?
A9B6C5D12 - Question 3 - Select One
OABC is a parallelogram such that OA=a,OB=bandOC=c, then the value →OA.→BA is
Aa2+3b2+c22Ba2−b2+3c22Ca2+3b2−c22D3a2+b2−c22
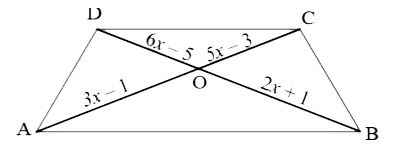
In the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
 View Solution
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8cm and BD=13.6cm. Find the measures of OC and OD.
View SolutionIf O is a point within a quadrilateral ABCD, show that OA+OB+OC+OD>AC+BD.
View SolutionIn a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :
View SolutionAn object is placed at A(OA>f). Here, f is the focal length of the lens. The image is formed at B. A perpendicular is erected at O and C is chosen such that ∠BCA=90∘. Let OA = a, OB = b and OC = c. Then the value of f is
View Solution

