In a Business school there are 3 electives offered to the students, where students have a choice of not choosing any electives. 70% students opted for Marketing, 60% students opted for HR and 50% students opted for Finance. 30% students opted for Marketing and HR both, 40% opted for HR and Finance both, 20% opted for Marketing and Finance both. What is the maximum number of students opted for all 3 electives?
To solve the problem step by step, we will use the principle of inclusion-exclusion to find the maximum number of students who opted for all three electives.
Step 1: Define the percentages for each elective
Let:
- M = percentage of students opting for Marketing = 70%
- H = percentage of students opting for HR = 60%
- F = percentage of students opting for Finance = 50%
Step 2: Define the percentages for combinations of two electives
Let:
- MH = percentage of students opting for both Marketing and HR = 30%
- HF = percentage of students opting for both HR and Finance = 40%
- MF = percentage of students opting for both Marketing and Finance = 20%
Step 3: Use the principle of inclusion-exclusion
The formula for the union of three sets is given by:
|M∪H∪F|=|M|+|H|+|F|−|MH|−|HF|−|MF|+|MHF|
Where |MHF| is the percentage of students opting for all three electives.
Step 4: Substitute the known values
Substituting the known values into the formula:
|M∪H∪F|=70+60+50−30−40−20+|MHF|
This simplifies to:
|M∪H∪F|=180−90+|MHF|
|M∪H∪F|=90+|MHF|
Step 5: Determine the maximum number of students
Since the total percentage of students cannot exceed 100%, we set up the equation:
90+|MHF|≤100
From this, we can solve for |MHF|:
|MHF|≤100−90
|MHF|≤10
Conclusion
The maximum number of students who opted for all three electives is 10%.
Let:
- M = percentage of students opting for Marketing = 70%
- H = percentage of students opting for HR = 60%
- F = percentage of students opting for Finance = 50%
Let:
- MH = percentage of students opting for both Marketing and HR = 30%
- HF = percentage of students opting for both HR and Finance = 40%
- MF = percentage of students opting for both Marketing and Finance = 20%
The formula for the union of three sets is given by:
|M∪H∪F|=|M|+|H|+|F|−|MH|−|HF|−|MF|+|MHF|
Where |MHF| is the percentage of students opting for all three electives.
Substituting the known values into the formula:
|M∪H∪F|=70+60+50−30−40−20+|MHF|
This simplifies to:
|M∪H∪F|=180−90+|MHF|
|M∪H∪F|=90+|MHF|
Since the total percentage of students cannot exceed 100%, we set up the equation:
90+|MHF|≤100
From this, we can solve for |MHF|:
|MHF|≤100−90
|MHF|≤10
The maximum number of students who opted for all three electives is 10%.
Topper's Solved these Questions
Similar Questions
In a Business school there are 3 electives offered to the students, where students have a choice of not choosing any electives. 70% students opted for Marketing, 60% students opted for HR and 50% students opted for Finance. 30% students opted for Marketing and HR both, 40% opted for HR and Finance both, 20% opted for Marketing and Finance both. What is the minimum number of students opted for all 3 electives?
View Solution
What is the number of students who opted for dancing ?
View Solution
Knowledge Check
In the IGNOU (Indira Gandhi National Open University) there are total 16,000 students pursuing MBA, which offers the specialization only in Finance, HR and Marketing IGNOU accepts only Science, Commerce and Engineering Students for the two years course of MBA. The number of science. students is 166.66% of the Commerce students. Number of Engineering students is equal to the number of Science and Commerce students together. Each student can specialize in only one of the marketing , HR and Finance, 20% of Science students opted the Finance, which is 16.66% less than the no. of commerce students who opted Finance. The total Finance students is equal to 18% the total strength of the MBA students. 32% of Science students opted HR. Commerce students who opted HR is equal to 25% of total students specializing in Finance and Engineering students equal to 6.5% of the total strength of the MBA students opted HR.
The number of Engineering students who opted marketing is :A7850B7500C8850Dnone of theseIn a class of 50 students, 35 opted for Mathematics and 37 opted for Biology . How have opted for only Mathematics ? (Assume that each student has to opt for at least one of the subjects )
A15B17C13D19In a school 60% of the students are girls. If number of boys is 480, then what is the total number of students in the school?
A1200B840C96D1320

Find the central angle of total number of students who opted for History ?
View Solution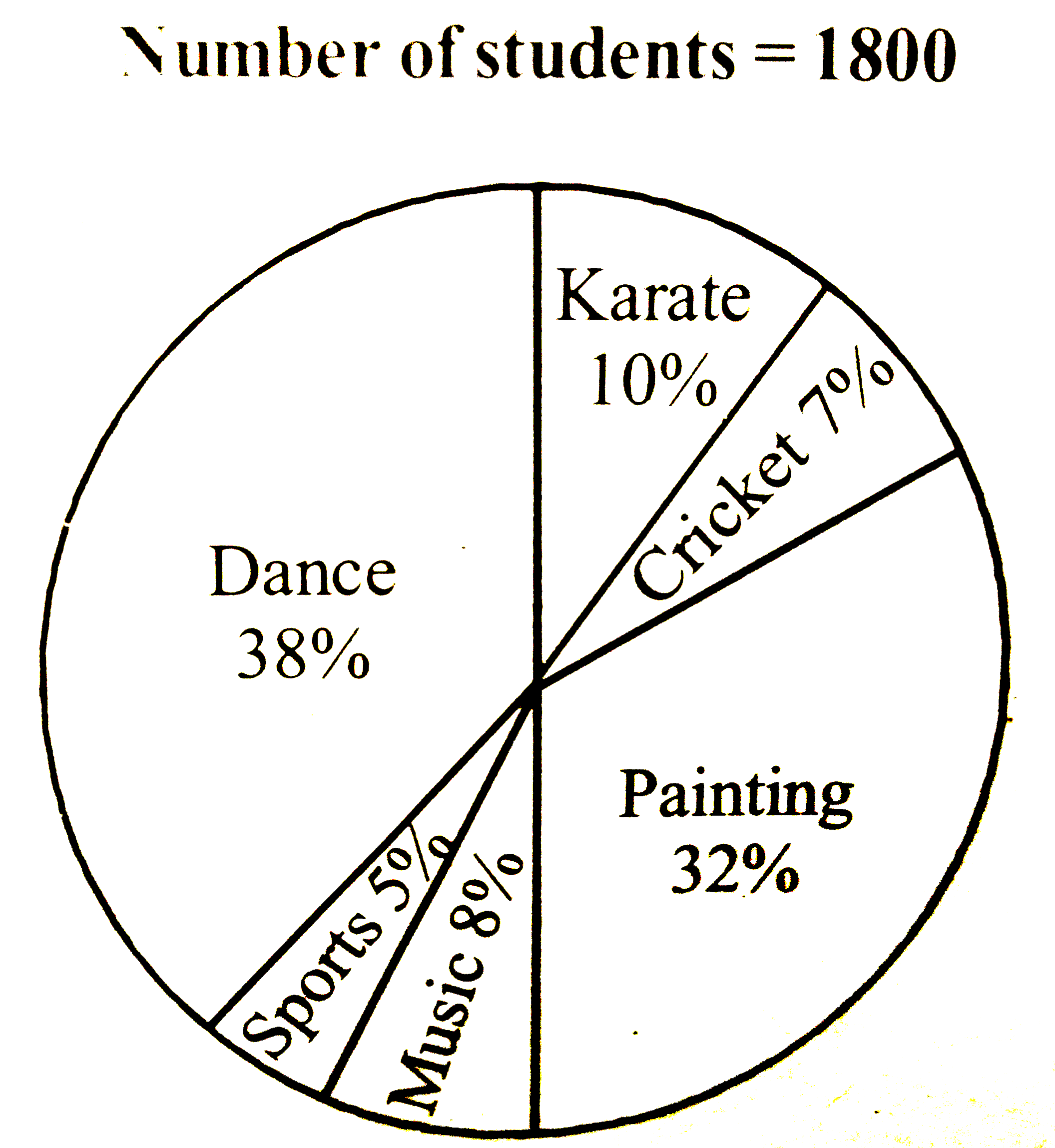
How many students have opted for cricket and painting together ?
View Solution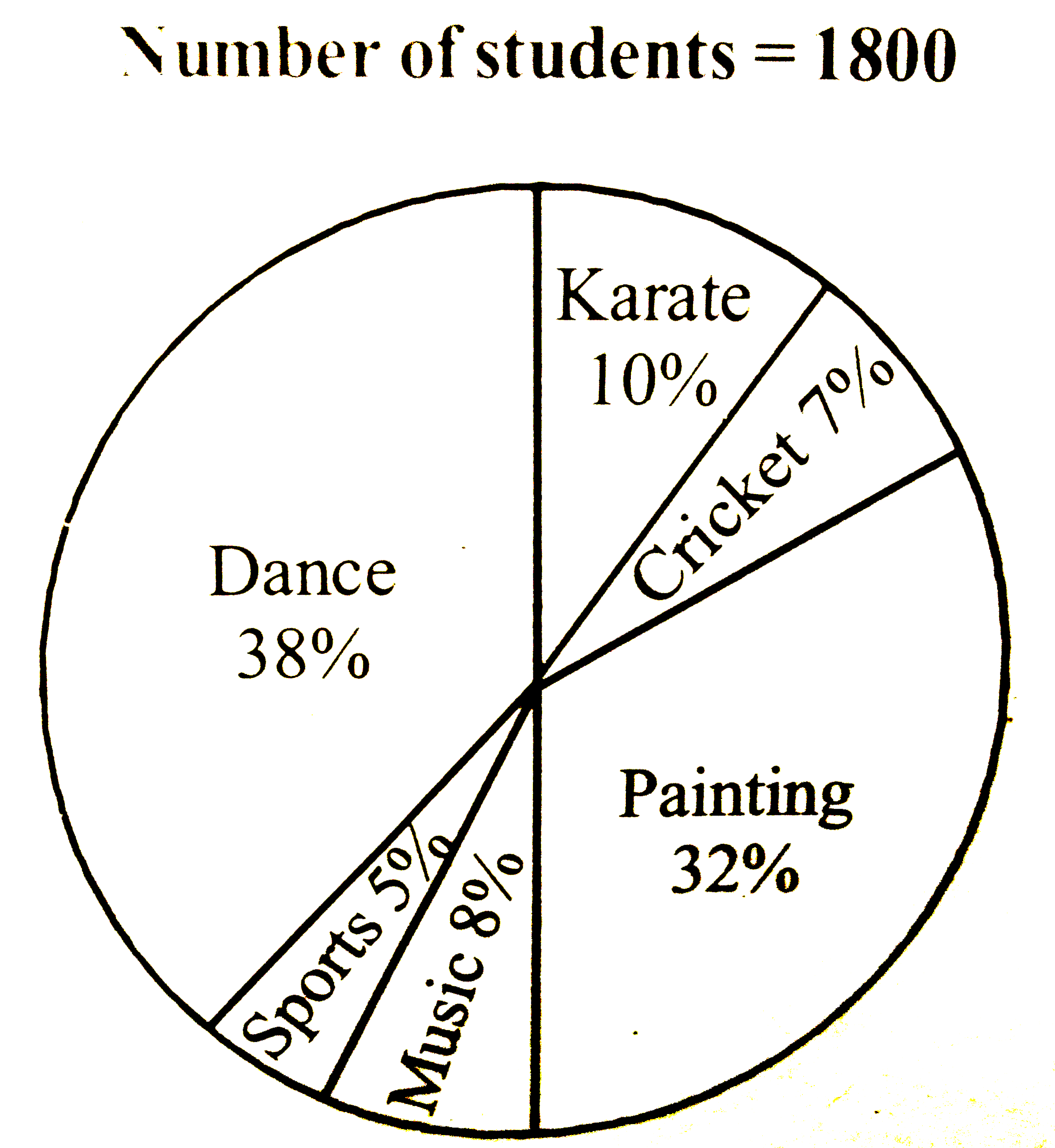
By What percent is the number of students who opted for cricket and dancing together more than those who opted for painting and music together ?
View Solution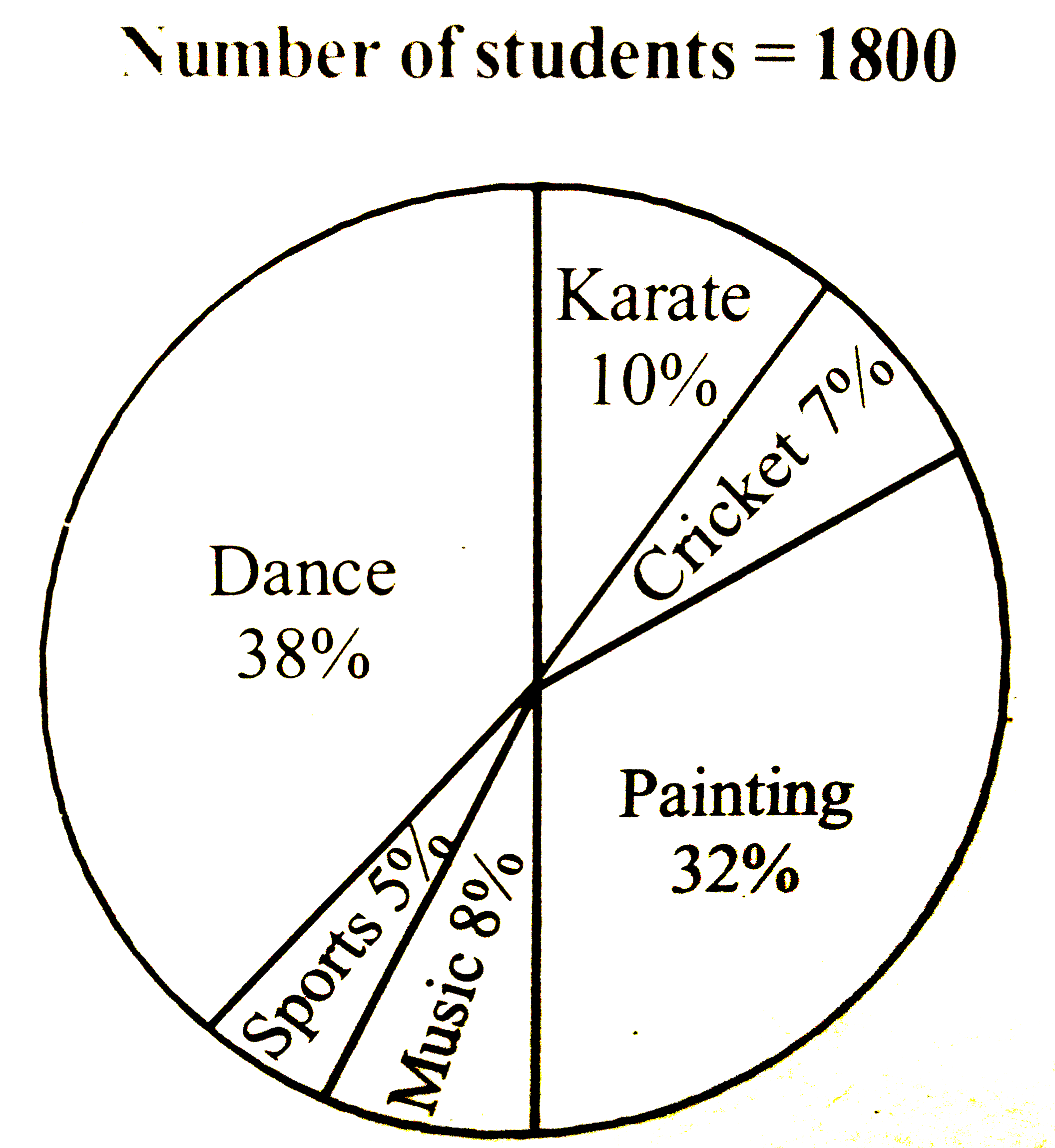
What is the respective ratio between the number of students who opted for painting and that who opted for Karate ?
View Solution
Find the average number of students who opted for Maths, Sociology and Sanskrit together ?
View Solution
