If the minimum value of the quadratic function is 0, then which of the following is not definitely true, about the roots?
Real
Non-Real'
Equal
Rational
The correct Answer is:B
To solve the problem, we need to analyze the properties of a quadratic function given that its minimum value is 0. A quadratic function can generally be expressed in the form:
f(x)=ax2+bx+c
where a, b, and c are constants, and a≠0.
Step 1: Understanding the Minimum Value
The minimum value of a quadratic function occurs at the vertex of the parabola. The x-coordinate of the vertex can be calculated using the formula:
x=−b2a
Given that the minimum value of the function is 0, we can conclude that:
f(−b2a)=0
This means that the function touches the x-axis at the vertex.
Step 2: Analyzing the Roots
Since the minimum value is 0, the quadratic function has a vertex that lies on the x-axis. The conditions for the roots of the quadratic function can be analyzed using the discriminant D:
D=b2−4ac
1. If D>0: There are two distinct real roots.
2. If D=0: There is one real root (a repeated root).
3. If D<0: There are no real roots (the roots are complex).
Step 3: Conclusion About the Roots
Since the minimum value is 0, we know that the quadratic function touches the x-axis at the vertex. This implies that:
- The quadratic has at least one real root (the vertex).
- The roots are equal (since it only touches the x-axis).
Step 4: Evaluating the Options
Now, let's evaluate the options given in the question:
1. Real Roots: This is definitely true because the function touches the x-axis.
2. Non-Real Roots: This is not true since we established that there is at least one real root.
3. Equal Roots: This is definitely true because the minimum value is 0, indicating a double root.
4. Rational Roots: This is not necessarily true. The roots can be irrational even if they are equal.
Final Answer
The option that is not definitely true about the roots is:
Non-real roots (Option 2) and Rational roots (Option 4).
The minimum value of a quadratic function occurs at the vertex of the parabola. The x-coordinate of the vertex can be calculated using the formula:
Since the minimum value is 0, the quadratic function has a vertex that lies on the x-axis. The conditions for the roots of the quadratic function can be analyzed using the discriminant D:
2. If D=0: There is one real root (a repeated root).
3. If D<0: There are no real roots (the roots are complex).
Since the minimum value is 0, we know that the quadratic function touches the x-axis at the vertex. This implies that:
- The roots are equal (since it only touches the x-axis).
Now, let's evaluate the options given in the question:
2. Non-Real Roots: This is not true since we established that there is at least one real root.
3. Equal Roots: This is definitely true because the minimum value is 0, indicating a double root.
4. Rational Roots: This is not necessarily true. The roots can be irrational even if they are equal.
The option that is not definitely true about the roots is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following is definitely true?
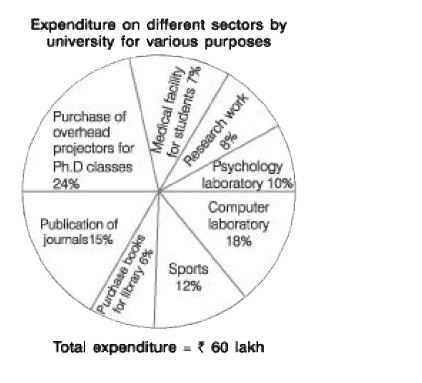 ARatio between expenditure of university on purchase of library books and expenditure on computer labor- atory is 3 : 1 respectivelyBExpenditure on medical facilities for students is X 4.6 lakhCDifference between the expenditure on research and medical facilities for students is X 60000DAll are true
ARatio between expenditure of university on purchase of library books and expenditure on computer labor- atory is 3 : 1 respectivelyBExpenditure on medical facilities for students is X 4.6 lakhCDifference between the expenditure on research and medical facilities for students is X 60000DAll are trueWhich of the following statement is definitely true ?
AIn a rhombus, the diagonals are equal.BIn an isosceles trapezium, the diagonals bisect each other.CIn a kite, the diagonals are perpendicular to each other.DIn a trapezium on pair of opposite sides are parallel to each other.Which of the following statement is definitely true ?
AIn a rhombus, the diagonals are equalBIn an isosceles trapezium , the diagonals bisect each otherCIn a kite, the diagonals are perpendicular to each otherDIn a trapezium on pair of opposite sides are paraller to each other
Which of the following is/are true about functional structure?
View SolutionIf the roots of a quadratic equation are real and unequal, which one of the following is necessarily true?
View SolutionWhich of the following sentences is not true about the functions of leaves?
View SolutionIf f(0)=f(1)=f(2)=0 and function f(x) is twice differentiable in (0, 2) and continuous in [0, 2], then which of the following is/are definitely true ?
View SolutionIf the roots of a quadratic equation are unequal, which one of the following cannot be true?
View Solution
