Consider a cylinder of height h cm and radius r=4π cm as shown in figure A string of certain length when wound on its cylindrical surface , starting at point A, gives a maximum of n turns .
What is the vertical spacing ( in cm ) between two consecutive turns ?
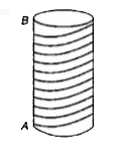
hn
√hn
h2n
can't be determined
The correct Answer is:A
Step by step video & image solution for Consider a cylinder of height h cm and radius r=(4)/(pi) cm as shown in figure A string of certain length when wound on its cylindrical surface , starting at point A, gives a maximum of n turns . What is the vertical spacing ( in cm ) between two consecutive turns ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid cylinder has radius of base 14 cm and height 15 cm, 4 identical cylinder are cut from each base as shown in the given figure. Height of small cylinder is 5 cm. What is the total surface area (in cm2) of the remaining part ?
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 100 cm, and its base is of radius 7 cm, find the total surface area of the article.

View Solution
Knowledge Check
Answer the questions on the basis of the information given Consider a cylinder of height h cm and radius r=2π cms as shown in the figure (not drawn to scale).
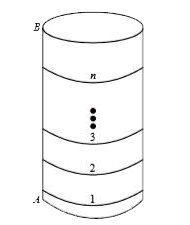
A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).
What is the vertical spacing in cms between two consecutive turns ?AA) h/nBB) h/√nCC) h/n2DD) Cannot be determined with given informationAnswer the questions on the basis of the information given Consider a cylinder of height h cm and radius r=2π cms as shown in the figure (not drawn to scale).
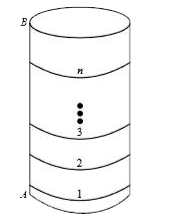
A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).
The same string, when wound on the exterior four walls of a cube of side n cms, starting at point C and ending at point D, can give exactly one turn (see figure, not drawn to scale)/ The length of the string, in cms, is
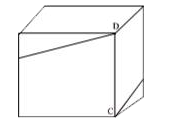 A√2nB√17nCnD√13n
A√2nB√17nCnD√13nAnswer the questions on the basis of the information given Consider a cylinder of height h cm and radius r=2π cms as shown in the figure (not drawn to scale).

A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).
In the setup of the previous two questions, how is h related to nAh=√2nBh=√17nCh =nDh=√13n
A circular cylinder of height h0=10cm and radius r0=2 cm is opened at the top and filled with liquid. It is rotated about its vertical axis. Determine the speed of rotation so that half the area of the bottom gets exposed (g=10m/s2):
View SolutionA circular ring of radius 5 cm is suspended horizontally from a point 12 cm vertically above its centre by 6 strings attached to its circumference at equal intervals. The cosine of the angle between two consecutive ring is
View SolutionA circular ring of radius 3 cm is suspended horizontally from a point 4 cm vertically above the centre by 4 strings attached at equal intervals to its cirumference . If the angle between two consecutive strings be θ, then cos(θ)-
View SolutionFind the length of the string wound on a cylinder of height 48 cm and a base diameter of 5111 cm. The string makes exactly four complete turns round the cylinder while its two ends touch the cylinder’s top and bottom.
View SolutionIf the string length of n is wound on the exterior four walls of a cube of side a cm starting at point C and ending at point D exactly above C , making equally spaced 4 turns . The side of the cube is :
View Solution
