In the adjoining figure a square of maximum possible area is circumscribed by the right angle triangle ABC in such a way that one of its side just lies on the hypotenuse of the triangle . What is the area of the square ?
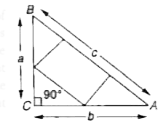
(baca2+b2+c2)2
a2+b2+c2abc
abca2+b2+c2
none of these
The correct Answer is:A
Step by step video & image solution for In the adjoining figure a square of maximum possible area is circumscribed by the right angle triangle ABC in such a way that one of its side just lies on the hypotenuse of the triangle . What is the area of the square ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the volume of the largest square (maximum area) that can be formed inside a triangle having side 3, 4, 5 such that one side of the square lies on the hypotenuse of the triangle.
View SolutionArea of a right-angled triangle is 30cm2. If its smallest side is 5 cm, then its hypotenuse is
View Solution
Knowledge Check
In the adjoining figure PQRS is a square of maximum possible area which is circumscribed by the semicricle . Points R and S lie on the diameter AB. What is the area of the square if the radius of the circle is 'r' ?
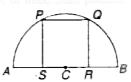 A√34r2B45r2C35r2D√54r2
A√34r2B45r2C35r2D√54r2In the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
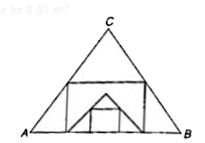 Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of these
Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of theseIn a right angle triangle ABC , what is the maximum possible area of a square that can be inscribed whe one of its vertices coincide with the vertex of righ angle of the triangle ?
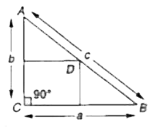 AabBaba+bCa+babD(aba+b)2
AabBaba+bCa+babD(aba+b)2
The area of an Isosceles right angled triangle is 32 square cms .Find the lengths of its sides ?
View SolutionThe base of a right-angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
View SolutionThe base of a right - angled triangle measures 48 cm and its hypotenuse measures 50 cm . Find the area of the triangle .
View SolutionIn a right angled triangle,if the sum of the squares of the sides making a right angle is 169, then what is the length of the hypotenuse?
View SolutionThe area of a right angled triangle is 24 cm and one of the sides containing the right angle is 6 cm. The altitude on the hypotenuse is
View Solution
