In a quadrant ( of a circle ) a circle of maximum possible area is given . If the radius of the circumscribing quadrant be r, then what is the area of the inscribed circle ?
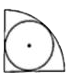
2+3√2)r2
πr23+2√2
(3+2√2r2)π
none of these
The correct Answer is:B
Step by step video & image solution for In a quadrant ( of a circle ) a circle of maximum possible area is given . If the radius of the circumscribing quadrant be r, then what is the area of the inscribed circle ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the area of right triangle if it is known that the radius of the circle inscribed in the triangle is r and that of the circumscribed circle is R.
View SolutionIn given figure ,a circle is inscribed in a square of side 4cm and an-other circle is circumscribing the square.prove that area of the cicumscribed circle two times the area of the inscribed circle.
View Solution
Knowledge Check
In the adjoining figure a quadrant ( of circle ) inscribes a square of maximum possible area . If the radius of the circle be 'r' then what is the area of the square ?
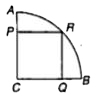 Ar22B3r25Cr2√3D2√6r
Ar22B3r25Cr2√3D2√6rIn the adjoining figure , AB is the diameter of a semicircle of maximum possible area . If the radius of the larger circle ( i.e, semicircle ) is r , the area of the inscribed circle is :
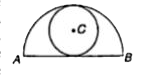 A5r2πB2π√3r2Cπr24Dnone of these
A5r2πB2π√3r2Cπr24Dnone of theseIf a triangle of maximum area is inscribed within a circle of radius R, then
 AS=2R2B1r1+1r2+1r3=√2+1RCr=(√2−1)RDs=(1+√2).2R
AS=2R2B1r1+1r2+1r3=√2+1RCr=(√2−1)RDs=(1+√2).2R
A triangle of maximum area is inscribed in a circle. If a side of the triangle is 20√3 then the radius of the circle is
View SolutionIf a triangle of maximum area is inscribed within a circle of radius R, then

View SolutionWhat is the area of a regular hexagon inscribed in a circle of radius r ?
View SolutionA semi-circle and a circle with same radius inscribe a square of greatest possible area. What is the ratio of area of square inscribed by semicircle to that by circle?
View SolutionThe difference of the area of the circumscribed and the inscribed square of a circle is 35 sq. cm. Find the area of the circle.
View Solution
