If f(x)=Sgn x and g(x)=1+x-[x], then for all x, f(g(x)) is equal to :
0
1
x
f(x)
The correct Answer is:B
To solve the problem, we need to evaluate f(g(x)) where f(x)=sgn(x) and g(x)=1+x−(x).
1. Understanding the Functions:
- The function f(x)=sgn(x) is defined as:
sgn(x)=⎧⎨⎩1if x>00if x=0−1if x<0
- The function g(x)=1+x−(x) can be simplified. Here, (x) denotes the greatest integer less than or equal to x. The term x−(x) represents the fractional part of x, which is always between 0 and 1. Therefore, g(x) can be rewritten as:
g(x)=1+(x−(x))=1+{x}
where {x} is the fractional part of x.
2. Range of g(x):
- Since {x} is always between 0 and 1, g(x) will always be:
g(x)=1+{x}∈(1,2)
- This means that g(x) is always greater than 1 for any real number x.
3. Evaluating f(g(x)):
- Now, we need to find f(g(x)). Since g(x)>1 for all x, we can substitute g(x) into f(x):
f(g(x))=f(1+{x})
- Since 1+{x}>0, we have:
f(g(x))=sgn(g(x))=1
4. Conclusion:
- Therefore, for all x, f(g(x))=1.
Final Answer:
f(g(x))=1for all x
- The function f(x)=sgn(x) is defined as:
sgn(x)=⎧⎨⎩1if x>00if x=0−1if x<0
- The function g(x)=1+x−(x) can be simplified. Here, (x) denotes the greatest integer less than or equal to x. The term x−(x) represents the fractional part of x, which is always between 0 and 1. Therefore, g(x) can be rewritten as:
g(x)=1+(x−(x))=1+{x}
where {x} is the fractional part of x.
- Since {x} is always between 0 and 1, g(x) will always be:
g(x)=1+{x}∈(1,2)
- This means that g(x) is always greater than 1 for any real number x.
- Now, we need to find f(g(x)). Since g(x)>1 for all x, we can substitute g(x) into f(x):
f(g(x))=f(1+{x})
- Since 1+{x}>0, we have:
f(g(x))=sgn(g(x))=1
- Therefore, for all x, f(g(x))=1.
f(g(x))=1for all x
Topper's Solved these Questions
Similar Questions
Let g(x)=1+x−[x]andf(x)={−1,x<00,x=0f,x>0. Then for all x,f(g(x)) is equal to (where [.] represents the greatest integer function). (a) x (b) 1 (c) f(x) (d) g(x)
View SolutionLet g(x)=1=x−[x]andf(x)={−1,x<0,0,x=0and1,x>0, then for all x,f(g(x)) is equal to (i) x (ii) 1 (iii) f(x) (iv) g(x)
View Solution
Knowledge Check
Let g(x)=1+x-[x] and
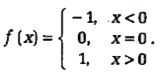 Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x)
Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x)If f(x) = 3x + 1 and g(x) =x2−1, then (f + g) (x) is equal to
Ax2+3xBx2−3x+2Cx2+3x+2Dx2−3xIf f(x) = 7x + 9 and g(x) =7x2−3, then (f - g)(x) is equal to
A7(x + 1)B7x−7x2+12C7x−7x2−12D7x2+7x−12
If f(x)=|x−2|andg(x)=f(f(x)), then for 2<x<4,g(x) equals
View SolutionIf f(x)=|x−2| and g(x)=f(f(x)), then for x>20,g'(x) equals
View SolutionIf f(x)=|x−1| and g(x)=f(f(f(x))), then for x>2,g'(x) is equal to
View SolutionIf f(x)=|x−2| and g(x)=f(f(x)), then for 2<x<4,g'(x) equals
View SolutionLet g(x)=1+x−[x]andf(x)=⎧⎪⎨⎪⎩−1,x<00,x=01,x>0, then for all x,f[g(x)] is equal to
View Solution
