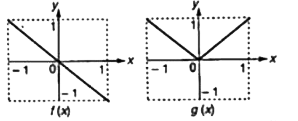
In each question there are two graphs f(x) and g(x) for the real value of x.
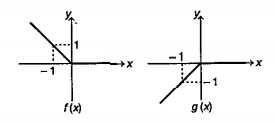
if g(x)=f(-x)
if g(x)=-f(x)
if g(x)=|f(x)|
none of these
The correct Answer is:B
Step by step video & image solution for In each question there are two graphs f(x) and g(x) for the real value of x. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In each question there are two graphs f(x) and g(x) for the real values of x.
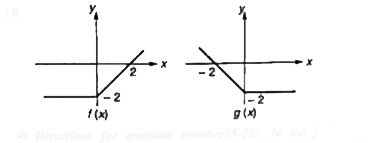 Aif g(x)=f(−x)BIf g(x)=−f(x)CIf g(x)=|f(x)|DIf none of the above is true.
Aif g(x)=f(−x)BIf g(x)=−f(x)CIf g(x)=|f(x)|DIf none of the above is true.In each question there are two graphs f(x) and g(x) for the real values of x.
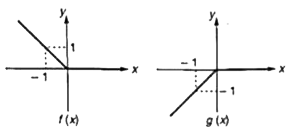 Aif g(x)=f(−x)BIf g(x)=−f(x)CIf g(x)=|f(x)|DIf none of the above is true.
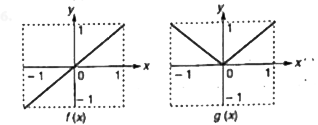
Aif g(x)=f(−x)BIf g(x)=−f(x)CIf g(x)=|f(x)|DIf none of the above is true.In each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
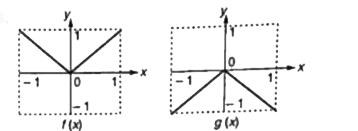 AA, if f(x)=−g(x) for every xBB. if f(x)=g(x) for x<0andf(x)=−g(x)x>0CC. if f(x)=−g(x) for x<0andf(x)=g(x),x>0DD. none of these
AA, if f(x)=−g(x) for every xBB. if f(x)=g(x) for x<0andf(x)=−g(x)x>0CC. if f(x)=−g(x) for x<0andf(x)=g(x),x>0DD. none of these
In each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
View SolutionIn each of the following questions a pair of graphs f(x) and g(x) is given, defined for every x∈(−1,1). Choose the correct answer as
View SolutionConsider that f:A→B
(i) If f(x) is one-one f(x1)=f(x2)⇔x1=x2 or f'(x)≥0 or f'(x)≤0.
(ii) If f(x) is onto the range of f(x) = B.
(iii) If f(x) and g(x) are inverse of each other then f(g(x)) = g(f(x)) = x.
Now consider the answer of the following questions.
If f(x) and g(x) are mirror image of each other through y = x and such that f(x) =ex+x then the value of g'(1) is
View SolutionThe absolute valued function f is defined as f(x)={xx≥0−xx<0} and fractional part function g(x) as g(x) = x-[x], graphically the number of real solution(s) of the equation f(x) = g(x) is obtained by finding the point(s) of interaction of the graph of y = f(x) and y = g(x).
The number of solutions (s) of |x−1|={x},x∈[−1,1] is
View SolutionThe absolute valued function f is defined as f(x)={xx≥0−xx<0} and fractional part function g(x) as g(x) = x-[x], graphically the number of real solution(s) of the equation f(x) = g(x) is obtained by finding the point(s) of interaction of the graph of y = f(x) and y = g(x).
The number of solution (s) |x−1|−|x+2|=k, when −3<k<3
View Solution
