Find the total number of rectangles when 8 vertical lines intersect 15 horizontal lines such that all the vertical lines are parallel and equidistant to each other, and all the horizontal lines are also parallel and equidistant to each other.
3996
6040
2940
6734
The correct Answer is:C
To find the total number of rectangles formed by 8 vertical lines and 15 horizontal lines, we can follow these steps:
1. Understanding the Problem:
We have 8 vertical lines and 15 horizontal lines. To form a rectangle, we need to select 2 vertical lines and 2 horizontal lines.
2. Selecting Vertical Lines:
The number of ways to select 2 lines from 8 vertical lines can be calculated using the combination formula nCk, which is given by:
nCk=n!k!(n−k)!
Here, n=8 and k=2:
8C2=8!2!(8−2)!=8!2!⋅6!
Simplifying this:
8C2=8×72×1=28
3. Selecting Horizontal Lines:
Similarly, the number of ways to select 2 lines from 15 horizontal lines is:
15C2=15!2!(15−2)!=15!2!⋅13!
Simplifying this:
15C2=15×142×1=105
4. Calculating Total Rectangles:
The total number of rectangles can be found by multiplying the number of ways to choose the vertical lines by the number of ways to choose the horizontal lines:
Total Rectangles=8C2×15C2=28×105
5. Performing the Multiplication:
Now, we calculate:
28×105=2940
6. Conclusion:
Therefore, the total number of rectangles formed by the intersection of 8 vertical lines and 15 horizontal lines is 2940.
We have 8 vertical lines and 15 horizontal lines. To form a rectangle, we need to select 2 vertical lines and 2 horizontal lines.
The number of ways to select 2 lines from 8 vertical lines can be calculated using the combination formula nCk, which is given by:
nCk=n!k!(n−k)!
Here, n=8 and k=2:
8C2=8!2!(8−2)!=8!2!⋅6!
Simplifying this:
8C2=8×72×1=28
Similarly, the number of ways to select 2 lines from 15 horizontal lines is:
15C2=15!2!(15−2)!=15!2!⋅13!
Simplifying this:
15C2=15×142×1=105
The total number of rectangles can be found by multiplying the number of ways to choose the vertical lines by the number of ways to choose the horizontal lines:
Total Rectangles=8C2×15C2=28×105
Now, we calculate:
28×105=2940
Therefore, the total number of rectangles formed by the intersection of 8 vertical lines and 15 horizontal lines is 2940.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the total number of squares when 8 vertical lines intersect 15 horizontal lines such that all the vertical lines are parallel and equidistant to each other, and all the horizontal lines are also parallel and equidistant to each other.
A336B456C1096D376 - Question 2 - Select One
Find the total number of quadrilaterals when 8 parallel lines intersect another set of 15 parallel lines.
A3636B2940C1990D3654
If two lines intersect each other, then the vertically opposite angles are equal.
View Solutionprove that two lines m and n be parallel to the same given line are parallel to each other.
View SolutionProve that two lines perpendicular to the same line are parallel to each other.
View SolutionFor what value of x will the lines l and m be parallel to each other ?
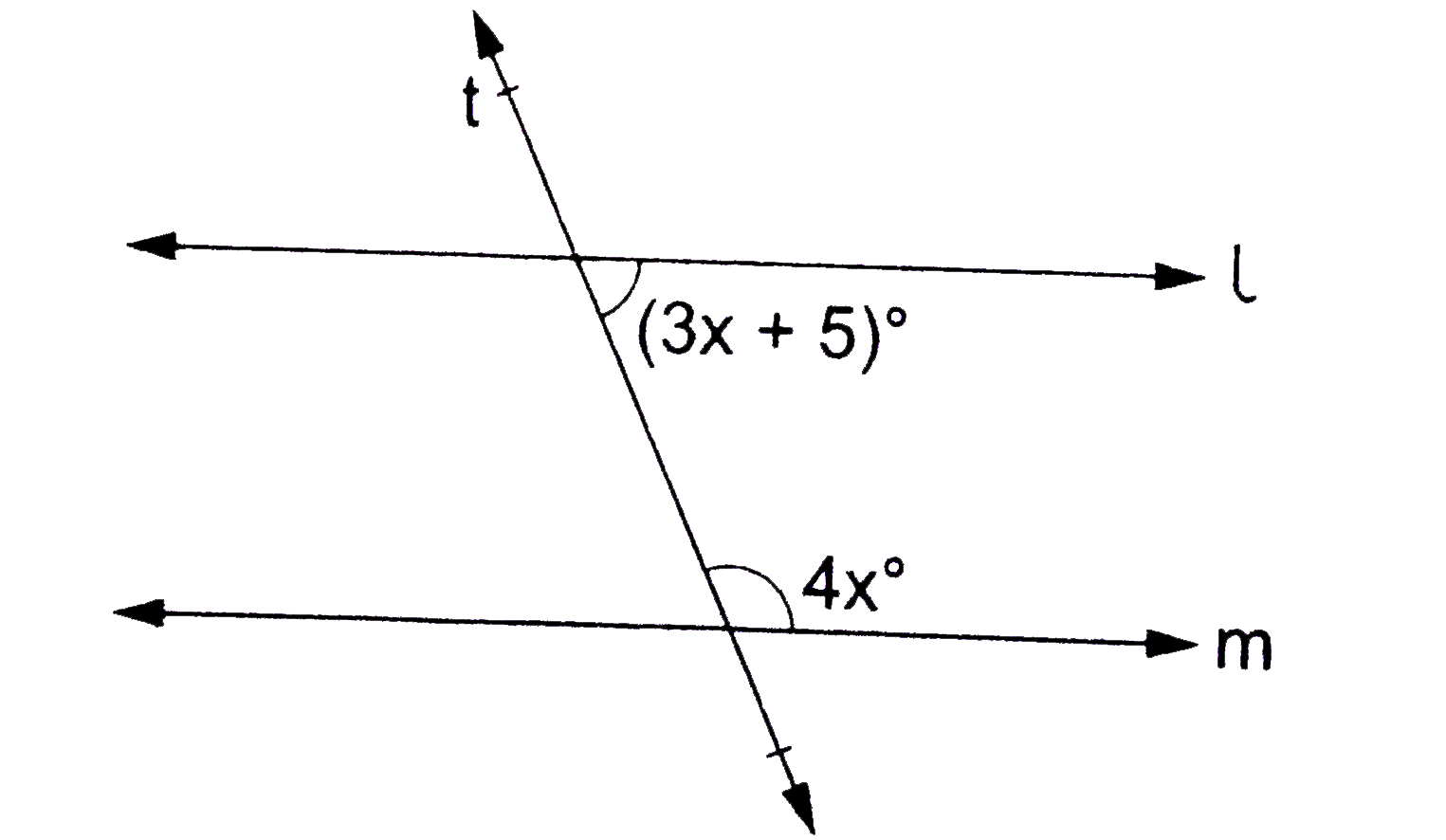 View Solution
View SolutionFor what value of x will the lines l and m be parallel to each other ?
 View Solution
View SolutionMagnetic lines of force intersect each other .
View Solution

