Find the total number of squares when 8 vertical lines intersect 15 horizontal lines such that all the vertical lines are parallel and equidistant to each other, and all the horizontal lines are also parallel and equidistant to each other.
336
456
1096
376
The correct Answer is:A
To find the total number of squares formed by 8 vertical lines and 15 horizontal lines, we can follow these steps:
Step 1: Understand the arrangement of lines
We have 8 vertical lines and 15 horizontal lines. The vertical lines are parallel and equidistant from each other, as are the horizontal lines.
Step 2: Determine the number of rows and columns
- The number of rows formed by the vertical lines is 8−1=7 (since the squares are formed between the lines).
- The number of columns formed by the horizontal lines is 15−1=14.
Step 3: Count the squares of different sizes
To find the total number of squares, we need to count squares of all possible sizes that can be formed:
1. 1x1 squares: The number of 1x1 squares is given by the product of the number of rows and columns:
1x1 squares=7×14=98
2. 2x2 squares: The number of 2x2 squares is given by:
2x2 squares=(7−1)×(14−1)=6×13=78
3. 3x3 squares: The number of 3x3 squares is given by:
3x3 squares=(7−2)×(14−2)=5×12=60
4. 4x4 squares: The number of 4x4 squares is given by:
4x4 squares=(7−3)×(14−3)=4×11=44
5. 5x5 squares: The number of 5x5 squares is given by:
5x5 squares=(7−4)×(14−4)=3×10=30
6. 6x6 squares: The number of 6x6 squares is given by:
6x6 squares=(7−5)×(14−5)=2×9=18
7. 7x7 squares: The number of 7x7 squares is given by:
7x7 squares=(7−6)×(14−6)=1×8=8
Step 4: Add all the squares together
Now, we will sum all the squares calculated:
Total squares=98+78+60+44+30+18+8
Calculating the total:
Total squares=98+78=176
176+60=236
236+44=280
280+30=310
310+18=328
328+8=336
Final Answer
The total number of squares formed is 336.
---
We have 8 vertical lines and 15 horizontal lines. The vertical lines are parallel and equidistant from each other, as are the horizontal lines.
- The number of rows formed by the vertical lines is 8−1=7 (since the squares are formed between the lines).
- The number of columns formed by the horizontal lines is 15−1=14.
To find the total number of squares, we need to count squares of all possible sizes that can be formed:
1x1 squares=7×14=98
2x2 squares=(7−1)×(14−1)=6×13=78
3x3 squares=(7−2)×(14−2)=5×12=60
4x4 squares=(7−3)×(14−3)=4×11=44
5x5 squares=(7−4)×(14−4)=3×10=30
6x6 squares=(7−5)×(14−5)=2×9=18
7x7 squares=(7−6)×(14−6)=1×8=8
Now, we will sum all the squares calculated:
Total squares=98+78+60+44+30+18+8
Total squares=98+78=176
176+60=236
236+44=280
280+30=310
310+18=328
328+8=336
The total number of squares formed is 336.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the total number of rectangles when 8 vertical lines intersect 15 horizontal lines such that all the vertical lines are parallel and equidistant to each other, and all the horizontal lines are also parallel and equidistant to each other.
A3996B6040C2940D6734 - Question 2 - Select One
Find the total number of quadrilaterals when 8 parallel lines intersect another set of 15 parallel lines.
A3636B2940C1990D3654
If two lines intersect each other, then the vertically opposite angles are equal.
View Solutionprove that two lines m and n be parallel to the same given line are parallel to each other.
View SolutionProve that two lines perpendicular to the same line are parallel to each other.
View SolutionFor what value of x will the lines l and m be parallel to each other ?
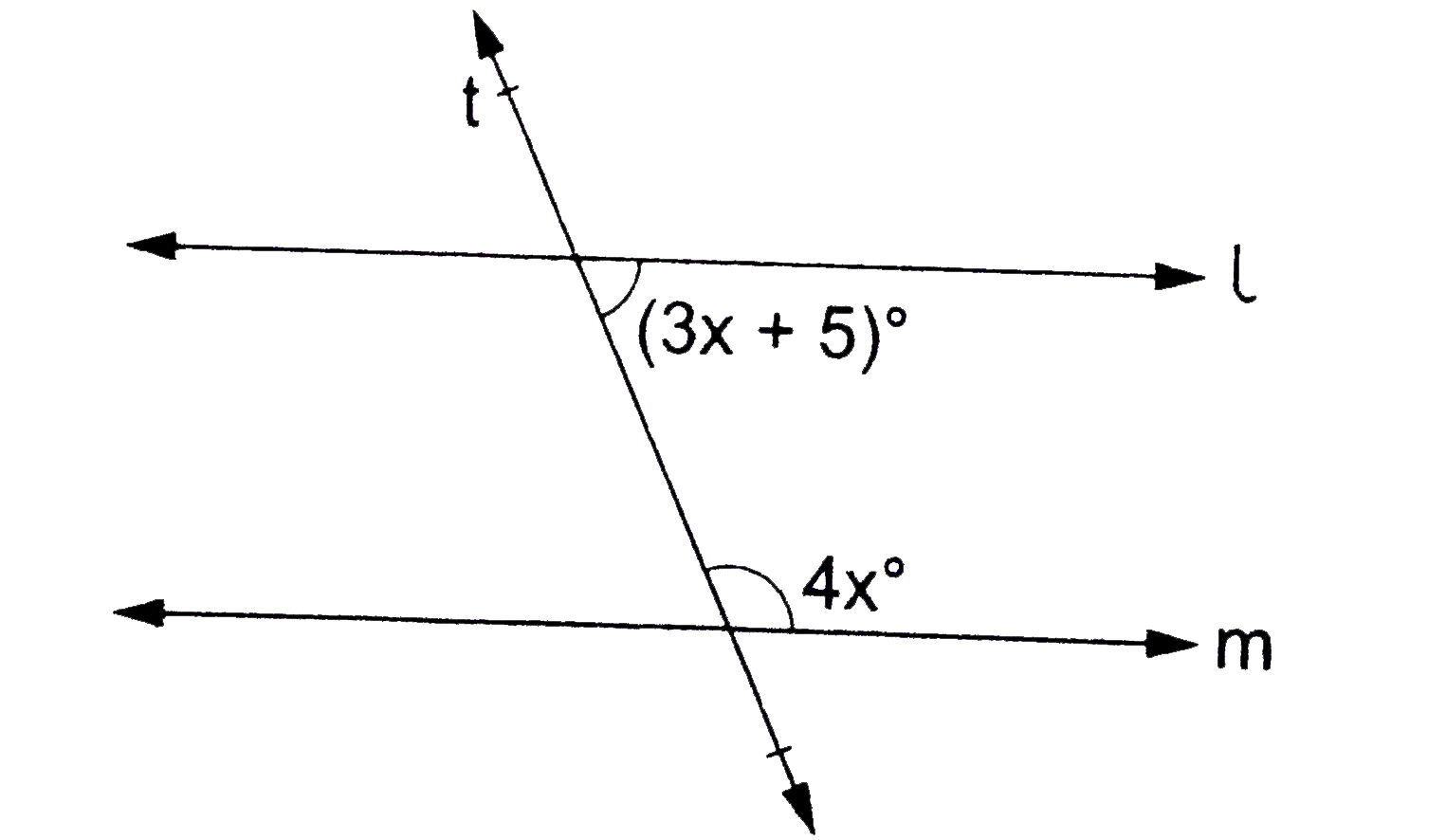 View Solution
View SolutionFor what value of x will the lines l and m be parallel to each other ?
 View Solution
View SolutionProve that if two lines intersect each other, then the vertically opposite angles are equal.
View Solution

