Derive function of 120∘ from functions of 60∘and check by using relations between functions of supplementary angles.
The correct Answer is:sin120∘=√32,cos120∘=−12,tan120∘=−√3
To derive the function of 120∘ from the function of 60∘ and verify it using the relations between functions of supplementary angles, we can follow these steps:
Step 1: Identify the angle
Let θ=60∘. We want to find sin(120∘).
Step 2: Use the double angle formula
We can express 120∘ in terms of 60∘ using the double angle formula:
sin(2θ)=2sin(θ)cos(θ)
Here, 2θ=120∘.
Step 3: Substitute θ
Substituting θ=60∘ into the double angle formula gives:
sin(120∘)=sin(2×60∘)=2sin(60∘)cos(60∘)
Step 4: Find the values of sin(60∘) and cos(60∘)
We know:
sin(60∘)=√32,cos(60∘)=12
Step 5: Substitute these values into the equation
Now substituting these values into the equation:
sin(120∘)=2(√32)(12)
Step 6: Simplify the expression
Simplifying the expression:
sin(120∘)=2⋅√32⋅12=√32
Step 7: Conclusion
Thus, we have derived that:
sin(120∘)=√32
Verification using supplementary angles
To verify, we can use the property of supplementary angles:
sin(180∘−θ)=sin(θ)
For θ=60∘:
sin(120∘)=sin(180∘−60∘)=sin(60∘)
Since sin(60∘)=√32, we have:
sin(120∘)=√32
Final Answer
Thus, the derived function of 120∘ is:
sin(120∘)=√32
And the verification confirms that our derived value is correct.
---
Let θ=60∘. We want to find sin(120∘).
We can express 120∘ in terms of 60∘ using the double angle formula:
sin(2θ)=2sin(θ)cos(θ)
Here, 2θ=120∘.
Substituting θ=60∘ into the double angle formula gives:
sin(120∘)=sin(2×60∘)=2sin(60∘)cos(60∘)
We know:
sin(60∘)=√32,cos(60∘)=12
Now substituting these values into the equation:
sin(120∘)=2(√32)(12)
Simplifying the expression:
sin(120∘)=2⋅√32⋅12=√32
Thus, we have derived that:
sin(120∘)=√32
To verify, we can use the property of supplementary angles:
sin(180∘−θ)=sin(θ)
For θ=60∘:
sin(120∘)=sin(180∘−60∘)=sin(60∘)
Since sin(60∘)=√32, we have:
sin(120∘)=√32
Thus, the derived function of 120∘ is:
sin(120∘)=√32
And the verification confirms that our derived value is correct.
Topper's Solved these Questions
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5 (D)
60 Videos
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - CHEPTER TEST
23 Videos
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5 (B)
35 Videos
- COMPLEX NUMBERSBOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Chapter Test
25 Videos
- CONIC SECTIONS BOOK - ICSECHAPTER - CONIC SECTIONS EXERCISE - Multiple Choice Questions
33 Videos
Similar Questions
Knowledge Check
Which of the following relations is a function?
AR= {(4,6), (3,9),(-11, 6), (3, 11)}BR = {(1,2), (2, 4), (2,6), (3,5)}CR = {(2,1),(4,3), (6,5), (8,7), (10,9)}DR= {(0,1),(1,3), (2,4), (3, 1), (3,5)}
Which among the following relations is a function ?
View SolutionRelation between graphs of a function and its inverse.
View SolutionWhich of the following relations are functions ? y<x+3.
View SolutionThe difference between two supplementary angles is 72∘ Find the angles.
View SolutionMatch the terms with related functions or terms:-

View SolutionGraph of functions are given in the following figure. Check the functions for absolute extremum.
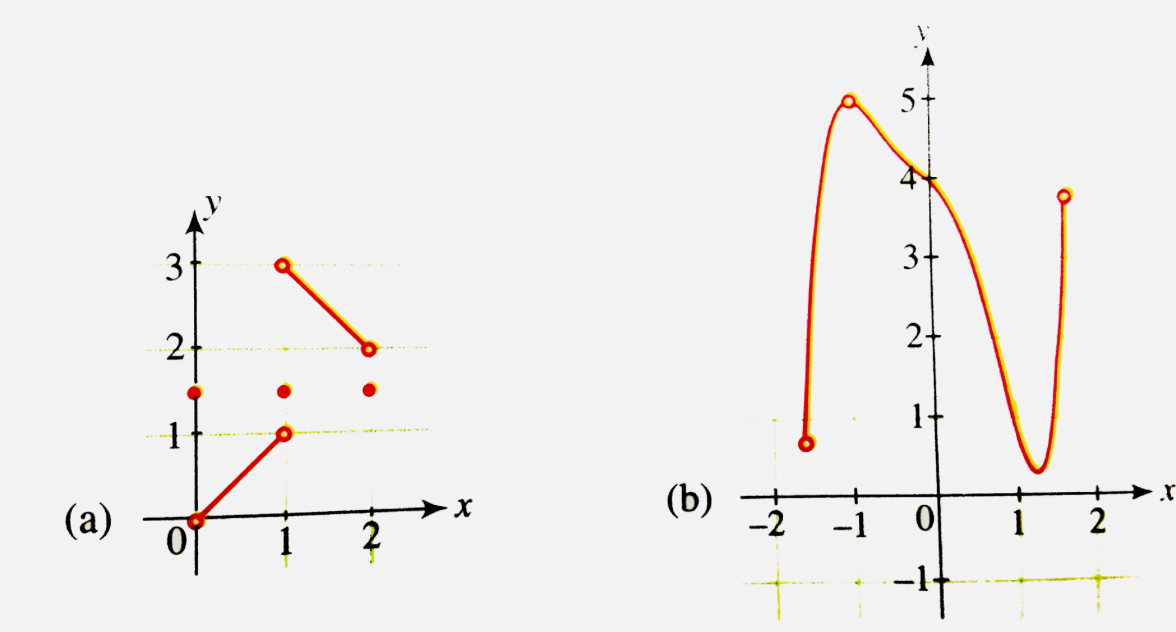
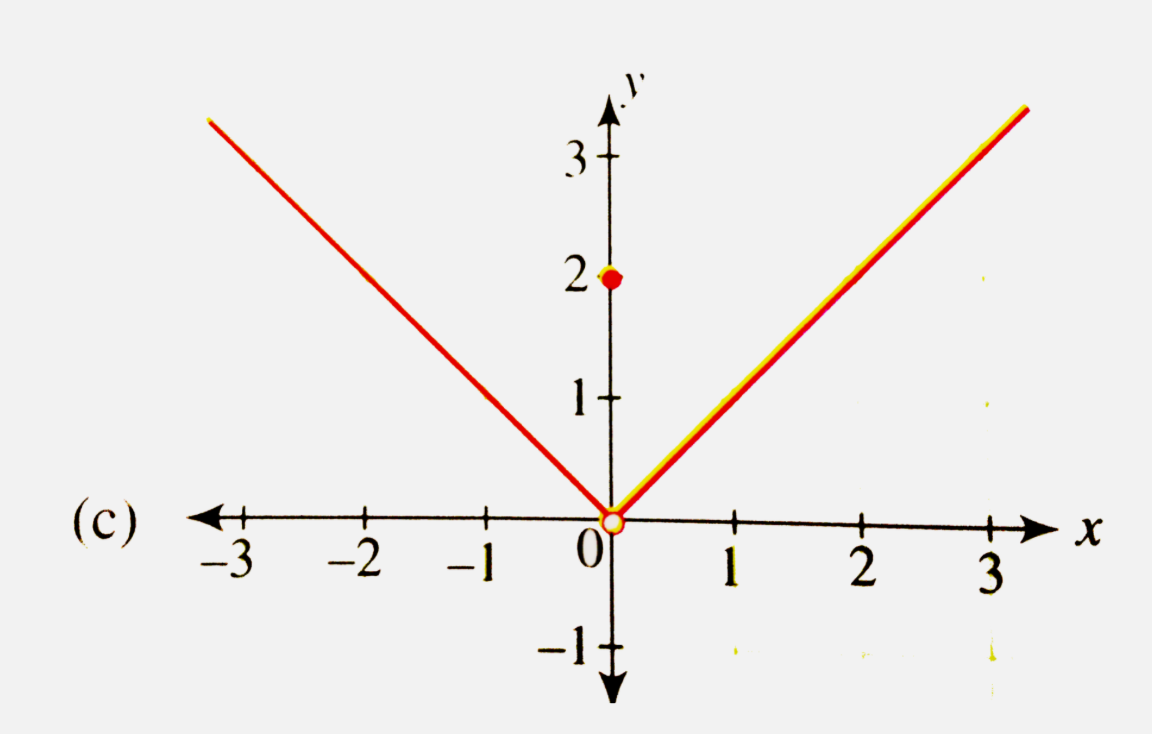
View SolutionObjective function of a LLP is
(A) a constraint
(B) a function to be optimized
(C) a relation between the variables
(D) none of these
View Solution
